Skip to content

Spacings

Given the order statistics X(1)≤...≤X(n)X_{(1)}\leq ... \leq X_{(n)}, define (n−1)(n-1) spacings (first order spacings) by

Dk=X(k+1)−X(k),k=1,...,n−1D_k = X_{(k+1)}-X_{(k)}, k=1,...,n-1

Intuitively, the spacings should carry some information about the pdf ff.

Note that if τ≈k+1n≈kn\tau \approx \frac{k+1}{n}\approx \frac{k}{n} then X(k+1)X_{(k+1)} and X(k)X_{(k)} estimate F−1(τ)F^{-1}(\tau).
If f(F−1(τ))f(F^{-1}(\tau)) is large then DkD_k is small, conversely, f(F−1(τ))f(F^{-1}(\tau)) is small then DkD_k is large.

Exponential Spacings

X1,...,Xn∼Exp(λ)X_1,...,X_n\sim Exp(\lambda) iid.

f(x;λ)=λexp⁡(−λx)I(x≥0)f(x;\lambda) = \lambda \exp(-\lambda x)\mathbb I(x\geq 0)

Given the order statistics X(1)≤...≤X(n)X_{(1)}\leq ...\leq X_{(n)} define

Y1=nX(1)Y2=(n−1)(X(2)−X(1))=(n−1)D1Y2=(n−2)(X(3)−X(2))=(n−2)D2⋮Yn=X(n)−X(n−1)=Dn−1\begin{align*} Y_1 &= nX_{(1)}\\ Y_2 &= (n-1)(X_{(2)}-X_{(1)}) = (n-1)D_1\\ Y_2 &= (n-2)(X_{(3)}-X_{(2)}) = (n-2)D_2\\ \vdots\\ Y_n &= X_{(n)} - X_{(n-1)} = D_{n-1} \end{align*}

Proposition 1

Y1,...,YnY_1,...,Y_n are iid ∼Exp(λ)\sim Exp(\lambda)

proof. Note that the join pdf of (X(1),...,X(n))(X_{(1)}, ..., X_{(n)}) if

f(x1,...,xn)=n!λnexp⁡(−λ∑nxi)I(0≤x1<x2<...<xn)f(x_1,...,x_n) = n!\lambda^n\exp(-\lambda \sum^n x_i)\mathbb I(0\leq x_1<x_2<...<x_n)

Also, note that

X(1)=Y1/nX(k)=Y1n+...+Ykn−k+1,k=2,...,n\begin{align*} X_{(1)} &= Y_1/n \\ X_{(k)} &= \frac{Y_1}{n} + ... + \frac{Y_k}{n-k+1}, k = 2,...,n \end{align*}

Therefore,

g(y1,...,yn)=f(y1n,...,y1n+y2n−1+...+yn)∣J(y1,...,yn)∣g(y_1,...,y_n) = f\big(\frac{y_1}n, ..., \frac{y_1}{n} + \frac{y_2}{n-1} + ... + y_n\big)|J(y_1,...,y_n)|

Note that ∣J∣|J| is the absolute determinant of the matrix

[1/n00...01/n1n−10...0⋮⋮⋱...⋮1/n1n−11n−2...1]\begin{bmatrix} 1/n&0&0&...&0\\ 1/n&\frac 1{n-1}&0&...&0\\ \vdots &\vdots &\ddots &...&\vdots\\ 1/n&\frac{1}{n-1}&\frac 1{n-2}&...&1 \end{bmatrix}

which is 1n!\frac{1}{n!}

g(y1,...,yn)=n!λnexp⁡(−λ∑nxi)1n!=λnexp⁡(−λ∑nxi)I(y1,...,yn≥0)g(y_1,...,y_n)=n!\lambda^n\exp(-\lambda \sum^n x_i) \frac 1{n!} = \lambda^n\exp(-\lambda \sum^n x_i)\mathbb I(y_1,...,y_n\geq 0)

Proposition 2

If knn→τ∈(0,1)\frac{k_n}n\rightarrow\tau\in (0,1) and f(F−1(τ))>0f(F^{-1}(\tau)) > 0, then

nDkn→dExp(f(F−1(τ)))nD_{k_n}\rightarrow^d Exp(f(F^{-1}(\tau)))
  ⟹  P(Dkn≤x)≈1−exp⁡(−nf(F−1(τ))x),x≥0\implies P(D_{k_n}\leq x )\approx 1 - \exp(-nf(F^{-1}(\tau))x), x\geq 0

proof. Note that

X(kn+1)=dF−1(E1+...+Ekn+1E1+...+En+1),X(kn)=dF−1(E1+...+EknE1+...+En+1)X_{(k_n+1)}=^d F^{-1}\big(\frac{E_1+...+E_{k_n+1}}{E_1+...+E_{n+1}}\big), X_{(k_n)}=^d F^{-1}\big(\frac{E_1+...+E_{k_n}}{E_1+...+E_{n+1}}\big)

where Ei∼Exp(1)E_i \sim Exp(1)
so that

nDkn=dn(F−1(E1+...+Ekn+1E1+...+En+1−F−1(E1+...+EknE1+...+En+1)))≈1f(F−1(τ))(nEkn+1E1+...+En+1)=1f(F−1(τ))(Ekn+1(E1+...+En+1)/n)→pEkn+1f(F−1(τ))WLLN, E1+...+En+1n→p1∼Exp(f(F−1(τ)))\begin{align*} nD_{k_n} &= ^d n\bigg(F^{-1}\big(\frac{E_1+...+E_{k_n+1}}{E_1+...+E_{n+1}} - F^{-1}\big(\frac{E_1+...+E_{k_n}}{E_1+...+E_{n+1}}\big)\big)\bigg)\\ &\approx \frac{1}{f(F^{-1}(\tau))}\bigg(\frac{nE_{k_n+1}}{E_1+...+E_{n+1}}\bigg)\\ &= \frac{1}{f(F^{-1}(\tau))}\bigg(\frac{E_{k_n+1}}{(E_1+...+E_{n+1})/n}\bigg)\\ &\rightarrow^p \frac{E_{k_n+1}}{f(F^{-1}(\tau))} &\text{WLLN, }\frac{E_1+...+E_{n+1}}n\rightarrow^p 1\\ &\sim Exp(f(F^{-1}(\tau))) \end{align*}

Example: density estimation using spacings

Consider D1,...,Dn−1D_1,...,D_{n-1} are iid. exponential with E(nDk)=exp⁡(g(Vk))E(nD_k) = \exp(g(V_k)) where Vk=X(k+1)+X(k)2V_k = \frac{X_{(k+1)} + X_{(k)}}{2}, then Vk≈F−1(τ),τ≈kn≈k+1nV_k\approx F^{-1}(\tau), \tau\approx \frac kn\approx \frac{k+1}n and the density is f(x)=exp⁡(−g(x))f(x)=\exp(-g(x))

Using B-spline functions, we can estimate the function g(x)g(x)

g(x)=β0+∑i=1pβjψj(x)g(x)=\beta_0 + \sum_{i=1}^p \beta_j \psi_j(x)

where βi\beta_i's are unknown parameters and ψj\psi_j's are B-spline functions. 

# create the splines functions
den.splines <- function(x,p=5) {
    library(splines)
    n <- length(x)
    x <- sort(x)
    x1 <- c(NA,x)
    x2 <- c(x,NA)
    sp <- (x2-x1)[2:n]
    mid <- 0.5*(x1+x2)[2:n]
    y <- n*sp
    xx <- bs(mid,df=p)
    r <- glm(y~xx,family=quasi(link="log",variance="mu^2"))
    density <- exp(-r$linear.predictors)
    r <- list(x=mid,density=density)
    r
}

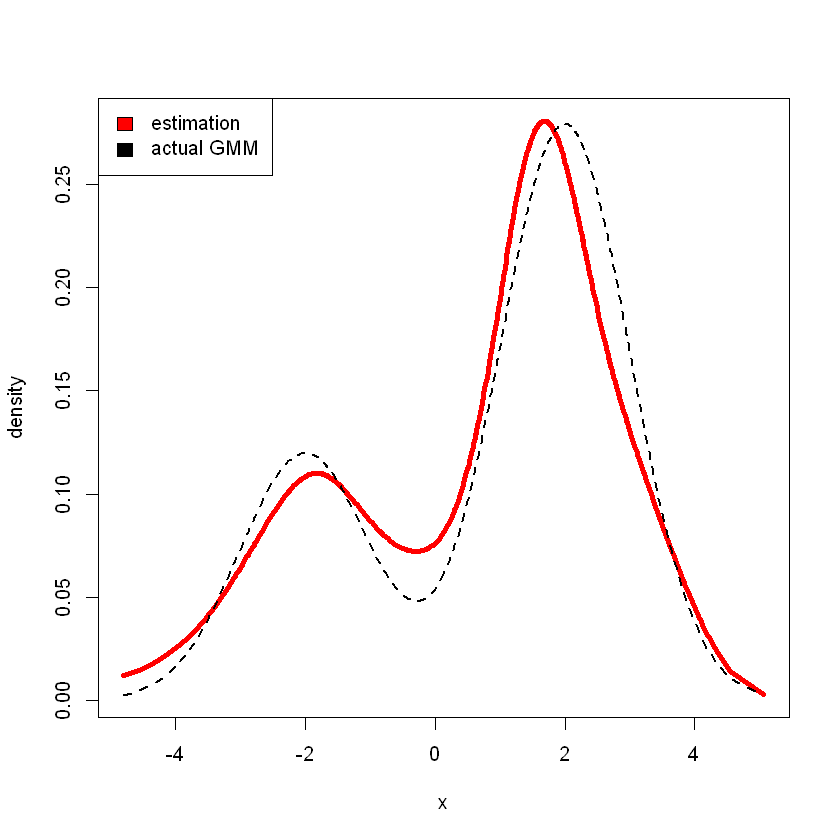
Consider sampling from GMM model

0.7N(2,1)+0.3N(−2,1)0.7N(2,1) + 0.3N(-2, 1)
# randomly sample 500 points from given GMM
x <- ifelse(runif(500) < .7, rnorm(500, 2, 1), rnorm(500, -2, 1))
# estimate density using p = 8
r <- den.splines(x,p=8)
# estimation
plot(r$x,r$density,type="l",xlab="x",ylab="density",lwd=4,col="red")
# actual
lines(r$x,0.3*dnorm(r$x,-2,1)+0.7*dnorm(r$x,2,1),lwd=2,lty=2)
legend("topleft", c("estimation", "actual GMM"), fill=c("red", "black"))

​

png

Hazard Functions

For XX is a positive continuous rv, its hazard function is

h(x)=f(x)1−F(x)h(x) = \frac{f(x)}{1-F(x)}

The motivation behind is to consider XX as the survival time, consider

δ−1P(x<X<x+δ∣X>x)=δ−1P(x<X≤x+δ)P(X>x)=δ−1F(x+δ)−F(x)1−F(x)→δ→0f(x)1−F(x)=:h(x)\begin{align*} \delta^{-1}P(x<X<x+\delta\mid X>x) &= \delta^{-1}\frac{P(x<X\leq x+\delta)}{P(X>x)}\\ &= \delta^{-1}\frac{F(x+\delta) - F(x)}{1-F(x)}\\ &\rightarrow_{\delta\rightarrow 0} \frac{f(x)}{1-F(x)} =:h(x) \end{align*}

Therefore, this represents instantaneous death rate given survival to time xx.

Also, note that

h(x)=f(x)1−F(x)=−ddxln⁡(1−F(x))h(x) = \frac{f(x)}{1-F(x)} = -\frac{d}{dx}\ln(1-F(x))

Therefore,

F(x)=1−exp⁡(−∫0xh(t)dt),f(x)=h(x)exp⁡(−∫0xh(t)dt)F(x) = 1 - \exp(-\int_0^x h(t)dt), f(x) = h(x)\exp(-\int_0^x h(t)dt)

In this case, we require ∫0∞h(x)dx=∞\int_0^\infty h(x)dx = \infty so that to have a "proper" probability distribution.

The shape of the hazard function gives info not immediately apparent in ff or FF. h(x)h(x) increasing indicates new better than used, decreasing indicates used better than new