Skip to content

Multi Comparisons and One Way ANOVA

Multiple Comparisons

  • post hoc procedure: further comparisons after significant result from overall One-way ANOVA
  • If the result for One-way ANOVA is good enough, i.e.some pairs are evidently true, we may omit some pairs to remove the number of tests
  • Max of (G2)G \choose 2 pairwise comparisons
  • Major issue: increased chance of making at least one Type I error when carrying out many tests, E(#errors)=#tests×αE(\#errors)=\#tests \times \alpha
  • Two common solutions: based on controlling family Type I error rate, choose
    • Bonferroni
    • Tukey's

Example P(committing at least 1 Type I error)P(\text{committing at least 1 Type I error}) ?

  • For n independent tests: P=1−(1−α)nP = 1-(1-\alpha)^n

Bonferroni's Method

  • Based on Bonferroni's inequality P(A∪B)≤P(A)+P(B)P(A\cup B) \leq P(A)+P(B), hence P(∪Ai)≤∑P(Ai),Ai:=P(\cup A_i)\leq \sum P(A_i), A_i:= the event that iith test results in a Type I error.
  • Method: conduct each of (k=G2)k=G \choose 2 pairwise tests at level α/k\alpha / k
  • CI: ∣yˉi−yˉj∣±tα/2kSpni−1+nj−1|\bar{y}_i - \bar{y}_j|\pm t_{\alpha/2k} S_p \sqrt{n_i^{-1} + n_j^{-1}}
  • Conservative: overall Type I error rate is usually much less than α\alpha if tests are not mutually independent.
  • Type II error inflation.

Tukey's Approach

  • Usually less conservative than Bonferroni, particularly if group sample size are similar. Controls the overall Type I error rate of α\alpha, simultaneous CI converage rate is 1−α1-\alpha.

Studentized Range distribution

  • X={X1,...,Xn},Xi∈N(μ,σ2)\mathcal{X}= \{X_1,...,X_n\}, X_i\in N(\mu,\sigma^2). Determine the distribution of the max and min of X\mathcal{X}.
  • X(n):=max⁡X,X(1);=min⁡XX_{(n)}:=\max{\mathcal{X}}, X_{(1)};=\min{\mathcal{X}}, Range :=X(n)−X(1):= X_{(n)}-X{(1)}
  • Based on nn observations from XX, the Studentized range statistic is Qstat=Range/s,s=Q_{stat} = Range / s, s= sample std.

  • Based on GG group means, with nn observations per group:

    Qˉg=n(yˉ(g)−yˉ(1))sv\bar{Q}_g = \frac{\sqrt{n}(\bar{y}_{(g)} - \bar{y}_{(1)})}{s_v}

svs_v estimator of the pooled std. v=N−G=G(n−1)v=N-G=G(n-1) d.f.

  • If there are GG groups, then there is a max of kk pairwise differences
  • Controlling overall simultaneous Type I error rate v.s. Individual Type I error rate
  • Find a pairwise significant difference
    • Compare method-wise significant difference, c(α)c(\alpha) with ∣yˉi−yˉj∣|\bar{y}_i - \bar{y}_j| OR
    • determine whether CI contains 0 OR
    • Compare pp with α\alpha
  • s=MSEs=\sqrt{MSE} with d.f. =v=d.f.Error=v=d.f.Error

Tukey's Honestly Significant Difference (HSD)

  • let q(G,v,α)/t∗:=q(G,v,\alpha)/t^*:= the critical value from the Studentized Range distribution.
  • Family rate =α=\alpha
  • Tukey's HSD =q(G,v,α)sn=q(G,v,\alpha) \frac{s}{\sqrt{n}}

Case Study

Bonferroni

  • H0:μi−μj=0,Ha:μi≠μjH_0:\mu_i - \mu_j = 0, H_a: \mu_i\neq \mu_j
  • t=xˉi−xˉjSpni−1+nj−1t = \frac{\bar{x}_i - \bar{x}_j}{S_p \sqrt{n_i^{-1} + n_j^{-1}}}
  • p=2P(Tα/2k>∣t∣)p = 2P(T_{\alpha/2k}> |t|)
# import data
library(Sleuth2)
jury = case0502
percent = case0502$Percent
judge = case0502$Judge

judge = relevel(judge, ref="Spock's")
pairwise.t.test(percent, judge, p.adj='bonf')

    Pairwise comparisons using t tests with pooled SD

data:  percent and judge

  Spock's A       B       C       D       E      
A 0.00022 -       -       -       -       -      
B 0.00013 1.00000 -       -       -       -      
C 0.00150 1.00000 1.00000 -       -       -      
D 0.57777 1.00000 1.00000 1.00000 -       -      
E 0.03408 1.00000 1.00000 1.00000 1.00000 -      
F 0.01254 1.00000 1.00000 1.00000 1.00000 1.00000

P value adjustment method: bonferroni

# CI
lmod=lm(percent~judge)
confint(lmod, level = 1- 0.05/nlevels(judge))
A matrix: 7 × 2 of type dbl
0.357 %99.643 %
(Intercept) 8.07808521.16636
judgeA 8.54734130.44821
judgeB 8.64725429.34163
judgeC 5.22296923.73259
judgeD-2.96958527.72514
judgeE 1.99725522.69163
judgeF 2.92297021.43259
 
amod = aov(percent~judge)
hsd = TukeyHSD(amod, 'judge')
hsd

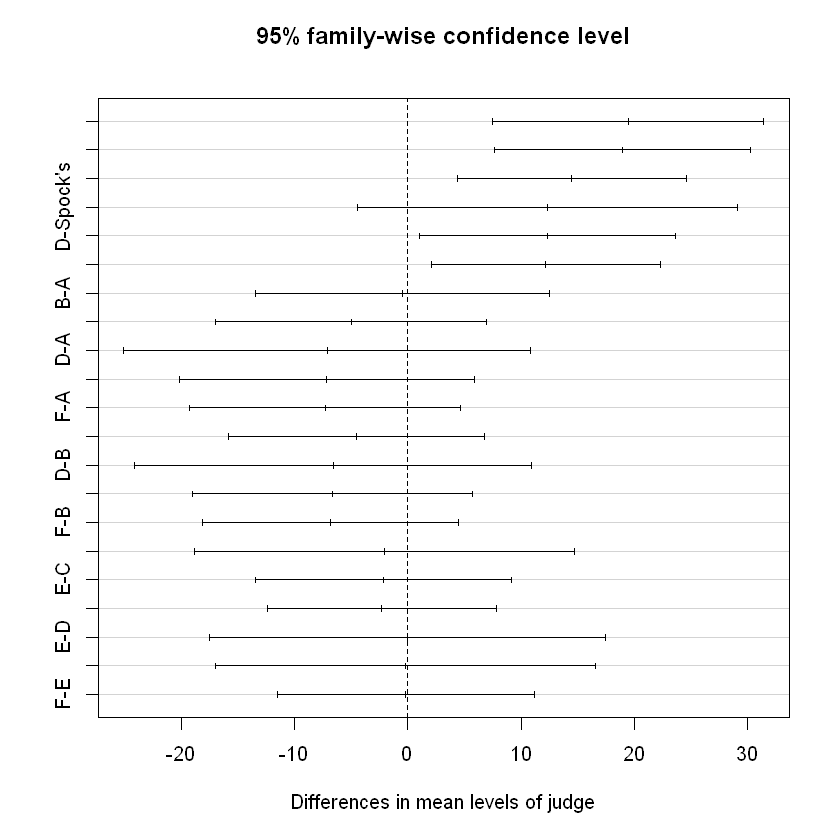
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = percent ~ judge)

$judge
                 diff        lwr       upr     p adj
A-Spock's 19.49777727   7.514685 31.480870 0.0001992
B-Spock's 18.99444405   7.671486 30.317402 0.0001224
C-Spock's 14.47777732   4.350216 24.605339 0.0012936
D-Spock's 12.37777758  -4.416883 29.172438 0.2744263
E-Spock's 12.34444443   1.021486 23.667402 0.0248789
F-Spock's 12.17777766   2.050216 22.305339 0.0098340
B-A       -0.50333322 -13.512422 12.505755 0.9999997
C-A       -5.01999995 -17.003092  6.963092 0.8470098
D-A       -7.11999969 -25.094638 10.854639 0.8777485
E-A       -7.15333284 -20.162421  5.855755 0.6146239
F-A       -7.31999961 -19.303092  4.663093 0.4936380
C-B       -4.51666673 -15.839625  6.806291 0.8742030
D-B       -6.61666648 -24.158118 10.924785 0.9003280
E-B       -6.64999962 -19.053679  5.753679 0.6418003
F-B       -6.81666639 -18.139624  4.506292 0.5109582
D-C       -2.09999975 -18.894661 14.694661 0.9996956
E-C       -2.13333289 -13.456291  9.189625 0.9968973
F-C       -2.29999966 -12.427561  7.827562 0.9914731
E-D       -0.03333314 -17.574784 17.508118 1.0000000
F-D       -0.19999992 -16.994661 16.594661 1.0000000
F-E       -0.16666677 -11.489625 11.156291 1.0000000

plot(hsd)

​

png

Linear Regression Model

  • YN×1=XN×(p+1)β(p+1)×1+ϵN×1Y_{N\times 1}=X_{N\times(p+1)}\beta_{(p+1)\times 1} + \epsilon_{N\times 1}, response YY continuous, explanatory XX categorical and/or continuous
  • YY is linear in the β\beta's i.e. no predictor is a linear function or combination of other predictors
  • β^=(X′X)−1X′Y\hat{\beta}=(X'X)^{-1}X'Y Least square Estimate, needrank(X′X)=rank(X)⇒rank(X'X)=rank(X)\Rightarrow columns of XX must be linear independent
  • Null hypothesis H0:β=0⃗H_0: \beta = \vec{0}. Assumptions
  • Appropriate Linear Model
  • Uncorrelated Errors
  • ϵ⃗∼N(0⃗,σ2I)\vec{\epsilon}\sim N(\vec{0},\sigma^2I).

  • Sum of Squares Decomposition

    SST=SSE+SSR∑iN(Yi−Yˉ)2=∑iN(Yi−Y^i)2+∑iN(Y^i−Yˉ)2\begin{align*}SST&=SSE+SSR\\ \sum_i^N(Y_i-\bar{Y})^2 &= \sum_i^N (Y_i-\hat{Y}_i)^2 + \sum_i^N(\hat{Y}_i - \bar{Y})^2 \end{align*}

One-Way ANOVA

  • Need one factor (categorical variable) with at least 2 levels (G≥2)(G\geq 2)

  • Aim: Compare GG group means

    H0:μ1=μ2=...=μG,Ha:∃i≠j.μi≠μjH_0:\mu_1=\mu_2=...=\mu_G, H_a:\exists i\neq j. \mu_i\neq \mu_j

  • Predictors are indicator variables that classify the observations one way (into GG groups)

    • special case of a general linear model
    • equivalent to GLM with one-way classification (one factor)
    • GLM uses G−1G-1 dummy variables
  • ANOVA: compare means by analyzing variability

One Way Expectations and Estimates

E(Yi)=(β0+β1,...,β0+βG−1,β0)TY^i=(b0+b1,...,b0+bG−1,b0)Tβ^=(b0,...,bG−1)T=(yˉG,yˉ1−yˉG,...,yˉG−1−yˉG)T\begin{align*} E(Y_i)&=(\beta_0 + \beta_1,...,\beta_0 +\beta_{G-1}, \beta_0)^T\\ \hat{Y}_i &= (b_0+b_1,...,b_0 + b_{G-1}, b_0)^T\\ \hat{\beta} &= (b_0,...,b_{G-1})^T = (\bar{y}_G, \bar{y}_1-\bar{y}_G,...,\bar{y}_{G-1}-\bar{y}_G)^T \end{align*}

Then, the null hypothesis is H0:βi=μi−μ0=0⇒H_0: \beta_i=\mu_i-\mu_0 = 0\Rightarrow the equal mean of iith group and the compared group

In this case, for SSTSST, N=∑1Gni,Y^i=N=\sum_1^G n_i,\hat{Y}_i= mean of observations for group gg from which the iith observation belongs, Yˉ=∑g=1G∑j=1ngygjN\bar{Y}=\frac{\sum_{g=1}^{G}\sum_{j=1}^{n_g} y_{gj}}{N} is the grand mean

SSReg=∑g=1Gng(Yˉg−Yˉ)2RSS=∑g=1G∑g(Yi−Yˉg)2\begin{align*} SSReg &= \sum_{g=1}^G n_g(\bar{Y}_g-\bar{Y})^2\\ RSS &= \sum_{g=1}^G \sum_{g} (Y_i-\bar{Y}_g)^2 \end{align*}
# import data
library(Sleuth2)
jury = case0502
percent = case0502$Percent
judge = case0502$Judge

table(judge)

judge
Spock's       A       B       C       D       E       F 
      9       5       6       9       2       6       9

with(jury, tapply(percent, judge, mean))

Spock's     14.6222224235535
A           34.1199996948242
B           33.6166664759318
C           29.0999997456868
D           27
E           26.9666668574015
F           26.800000084771

Compare 6 judges (exclude Spock)

others = subset(jury, judge != "Spock's") 
boxplot(others$Percent~others$Judge, data=others)

​

png

summary(aov(others$Percent~others$Judge))


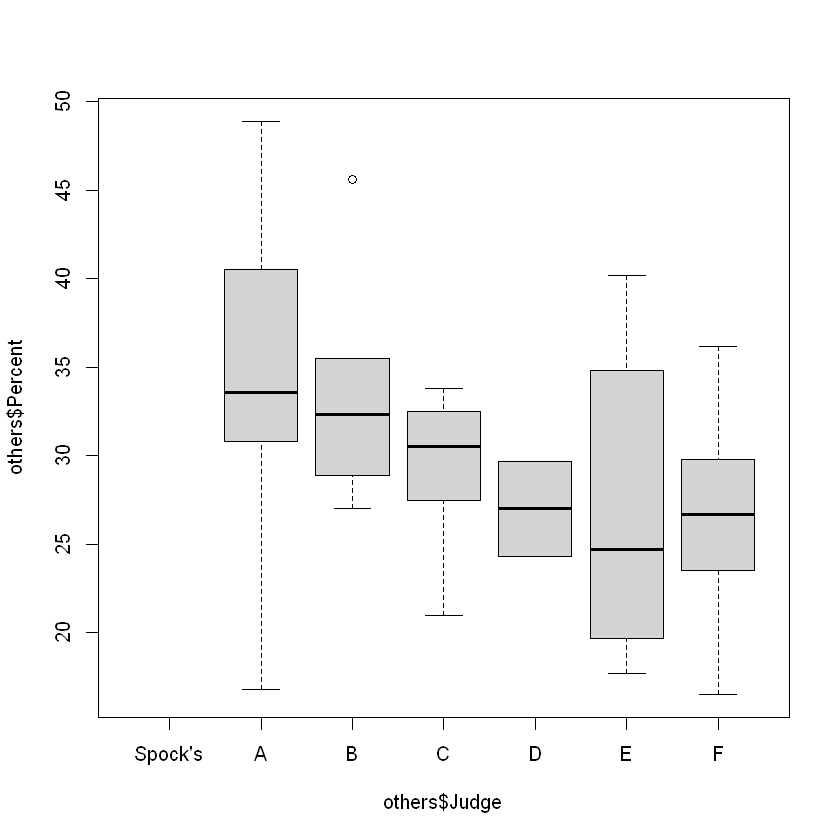
             Df Sum Sq Mean Sq F value Pr(>F)
others$Judge  5  326.5   65.29   1.218  0.324
Residuals    31 1661.3   53.59

Rule of thumb

Not a formal way, not a quick check whether equal variance

sss <- with(others, tapply(others$Percent, others$Judge, sd))
sss

Spock's     <NA>
A           11.9418181005452
B           6.58222301297842
C           4.59292918339244
D           3.81837769736668
E           9.01014223675898
F           5.96887758208529

max(sss, na.rm=T); min(sss, na.rm=T)

11.9418181005452
3.81837769736668

max(sss, na.rm=T) / min(sss, na.rm=T) > 2

TRUE

bartlett.test(others$Percent, others$Judge)

    Bartlett test of homogeneity of variances

data:  others$Percent and others$Judge
Bartlett's K-squared = 6.3125, df = 5, p-value = 0.277

The small p-value may due to the uneven and small group sizes

Compare all 7 judges

boxplot(percent~judge)

​

png 

summary(aov(percent~judge))

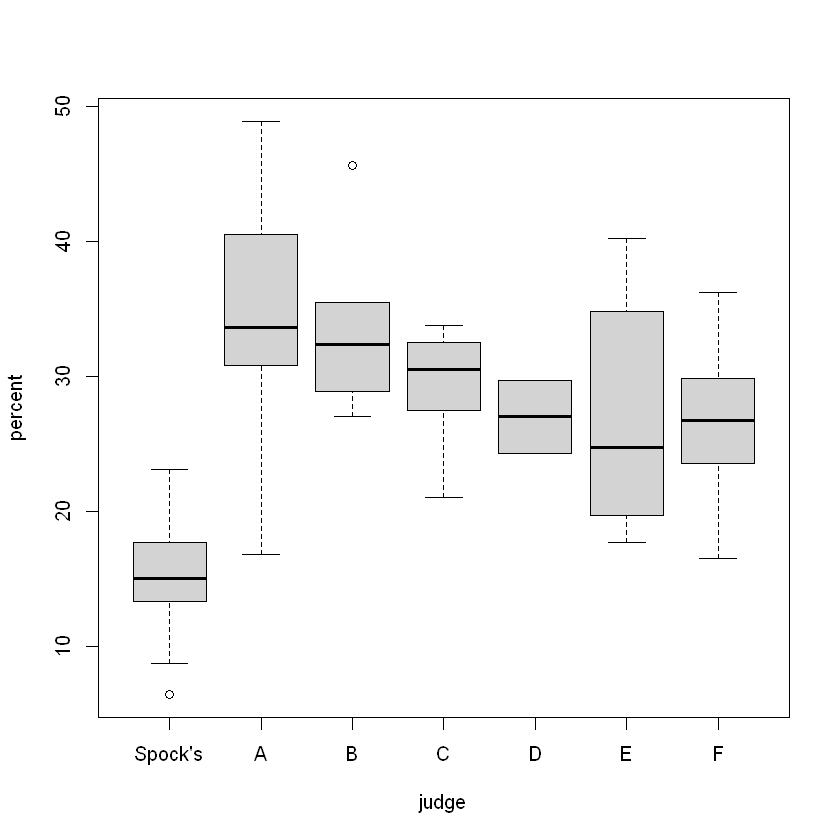
            Df Sum Sq Mean Sq F value  Pr(>F)    
judge        6   1927   321.2   6.718 6.1e-05 ***
Residuals   39   1864    47.8                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

summary(lm(percent~judge))

Call:
lm(formula = percent ~ judge)

Residuals:
    Min      1Q  Median      3Q     Max 
-17.320  -4.367  -0.250   3.319  14.780

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   14.622      2.305   6.344 1.72e-07 ***
judgeA        19.498      3.857   5.056 1.05e-05 ***
judgeB        18.994      3.644   5.212 6.39e-06 ***
judgeC        14.478      3.259   4.442 7.15e-05 ***
judgeD        12.378      5.405   2.290 0.027513 *  
judgeE        12.344      3.644   3.388 0.001623 ** 
judgeF        12.178      3.259   3.736 0.000597 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.914 on 39 degrees of freedom
Multiple R-squared:  0.5083,    Adjusted R-squared:  0.4326 
F-statistic: 6.718 on 6 and 39 DF,  p-value: 6.096e-05

par(mfrow=c(2,2))
plot(lm(percent~judge))

​

png 

ssa = with(jury, tapply(percent,judge,sd))
ssa

Spock's     5.03879411343757
A           11.9418181005452
B           6.58222301297842
C           4.59292918339244
D           3.81837769736668
E           9.01014223675898
F           5.96887758208529

max(ssa) / min(ssa) > 2

TRUE

bartlett.test(percent~judge)

    Bartlett test of homogeneity of variances

data:  percent by judge
Bartlett's K-squared = 7.7582, df = 6, p-value = 0.2564
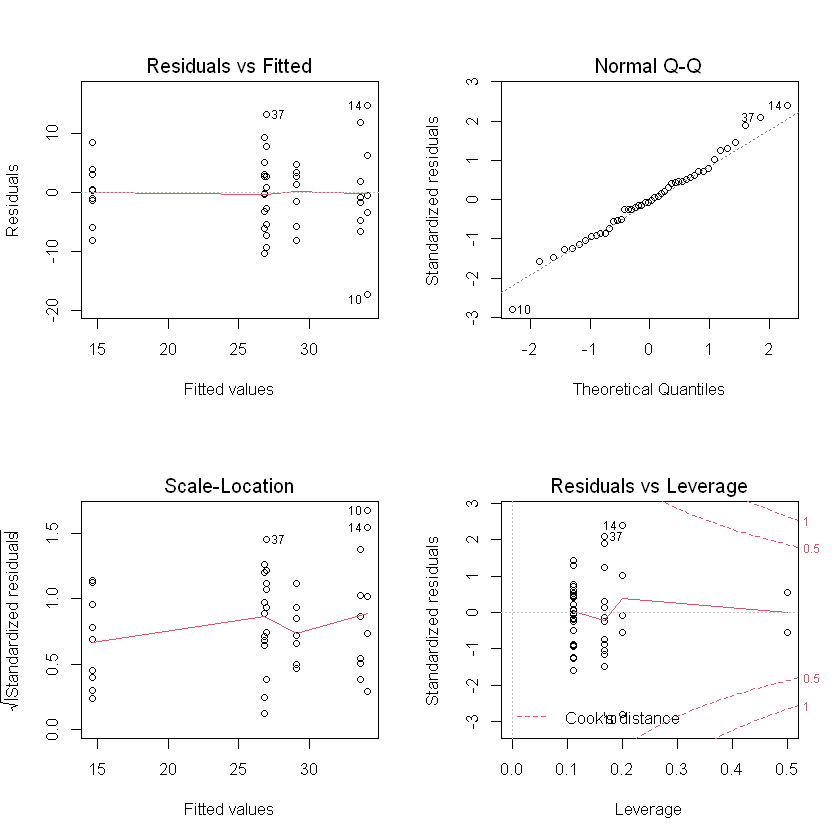
  • Residual vs Fitted: No obvious pattern, assume equal variance (also by rule of thumb and Bartlett)
  • Normal Q-Q: overall OK
  • Outliers: see Residual vs leverage, not influential point.

​

png