Skip to content

Spacings

Given the order statistics \(X_{(1)}\leq ... \leq X_{(n)}\), define \((n-1)\) spacings (first order spacings) by

\[D_k = X_{(k+1)}-X_{(k)}, k=1,...,n-1\]

Intuitively, the spacings should carry some information about the pdf \(f\).

Note that if \(\tau \approx \frac{k+1}{n}\approx \frac{k}{n}\) then \(X_{(k+1)}\) and \(X_{(k)}\) estimate \(F^{-1}(\tau)\).
If \(f(F^{-1}(\tau))\) is large then \(D_k\) is small, conversely, \(f(F^{-1}(\tau))\) is small then \(D_k\) is large.

Exponential Spacings

\(X_1,...,X_n\sim Exp(\lambda)\) iid.

\[f(x;\lambda) = \lambda \exp(-\lambda x)\mathbb I(x\geq 0)\]

Given the order statistics \(X_{(1)}\leq ...\leq X_{(n)}\) define

\[\begin{align*} Y_1 &= nX_{(1)}\\ Y_2 &= (n-1)(X_{(2)}-X_{(1)}) = (n-1)D_1\\ Y_2 &= (n-2)(X_{(3)}-X_{(2)}) = (n-2)D_2\\ \vdots\\ Y_n &= X_{(n)} - X_{(n-1)} = D_{n-1} \end{align*}\]

Proposition 1

\(Y_1,...,Y_n\) are iid \(\sim Exp(\lambda)\)

proof. Note that the join pdf of \((X_{(1)}, ..., X_{(n)})\) if

\[f(x_1,...,x_n) = n!\lambda^n\exp(-\lambda \sum^n x_i)\mathbb I(0\leq x_1<x_2<...<x_n)\]

Also, note that

\[\begin{align*} X_{(1)} &= Y_1/n \\ X_{(k)} &= \frac{Y_1}{n} + ... + \frac{Y_k}{n-k+1}, k = 2,...,n \end{align*}\]

Therefore,

\[g(y_1,...,y_n) = f\big(\frac{y_1}n, ..., \frac{y_1}{n} + \frac{y_2}{n-1} + ... + y_n\big)|J(y_1,...,y_n)|\]

Note that \(|J|\) is the absolute determinant of the matrix

\[\begin{bmatrix} 1/n&0&0&...&0\\ 1/n&\frac 1{n-1}&0&...&0\\ \vdots &\vdots &\ddots &...&\vdots\\ 1/n&\frac{1}{n-1}&\frac 1{n-2}&...&1 \end{bmatrix}\]

which is \(\frac{1}{n!}\)

\[g(y_1,...,y_n)=n!\lambda^n\exp(-\lambda \sum^n x_i) \frac 1{n!} = \lambda^n\exp(-\lambda \sum^n x_i)\mathbb I(y_1,...,y_n\geq 0)\]

Proposition 2

If \(\frac{k_n}n\rightarrow\tau\in (0,1)\) and \(f(F^{-1}(\tau)) > 0\), then

\[nD_{k_n}\rightarrow^d Exp(f(F^{-1}(\tau)))\]
\[\implies P(D_{k_n}\leq x )\approx 1 - \exp(-nf(F^{-1}(\tau))x), x\geq 0\]

proof. Note that

\[X_{(k_n+1)}=^d F^{-1}\big(\frac{E_1+...+E_{k_n+1}}{E_1+...+E_{n+1}}\big), X_{(k_n)}=^d F^{-1}\big(\frac{E_1+...+E_{k_n}}{E_1+...+E_{n+1}}\big)\]

where \(E_i \sim Exp(1)\)
so that

\[\begin{align*} nD_{k_n} &= ^d n\bigg(F^{-1}\big(\frac{E_1+...+E_{k_n+1}}{E_1+...+E_{n+1}} - F^{-1}\big(\frac{E_1+...+E_{k_n}}{E_1+...+E_{n+1}}\big)\big)\bigg)\\ &\approx \frac{1}{f(F^{-1}(\tau))}\bigg(\frac{nE_{k_n+1}}{E_1+...+E_{n+1}}\bigg)\\ &= \frac{1}{f(F^{-1}(\tau))}\bigg(\frac{E_{k_n+1}}{(E_1+...+E_{n+1})/n}\bigg)\\ &\rightarrow^p \frac{E_{k_n+1}}{f(F^{-1}(\tau))} &\text{WLLN, }\frac{E_1+...+E_{n+1}}n\rightarrow^p 1\\ &\sim Exp(f(F^{-1}(\tau))) \end{align*}\]

Example: density estimation using spacings

Consider \(D_1,...,D_{n-1}\) are iid. exponential with \(E(nD_k) = \exp(g(V_k))\) where \(V_k = \frac{X_{(k+1)} + X_{(k)}}{2}\), then \(V_k\approx F^{-1}(\tau), \tau\approx \frac kn\approx \frac{k+1}n\) and the density is \(f(x)=\exp(-g(x))\)

Using B-spline functions, we can estimate the function \(g(x)\)

\[g(x)=\beta_0 + \sum_{i=1}^p \beta_j \psi_j(x)\]

where \(\beta_i\)'s are unknown parameters and \(\psi_j\)'s are B-spline functions. 

# create the splines functions
den.splines <- function(x,p=5) {
    library(splines)
    n <- length(x)
    x <- sort(x)
    x1 <- c(NA,x)
    x2 <- c(x,NA)
    sp <- (x2-x1)[2:n]
    mid <- 0.5*(x1+x2)[2:n]
    y <- n*sp
    xx <- bs(mid,df=p)
    r <- glm(y~xx,family=quasi(link="log",variance="mu^2"))
    density <- exp(-r$linear.predictors)
    r <- list(x=mid,density=density)
    r
}

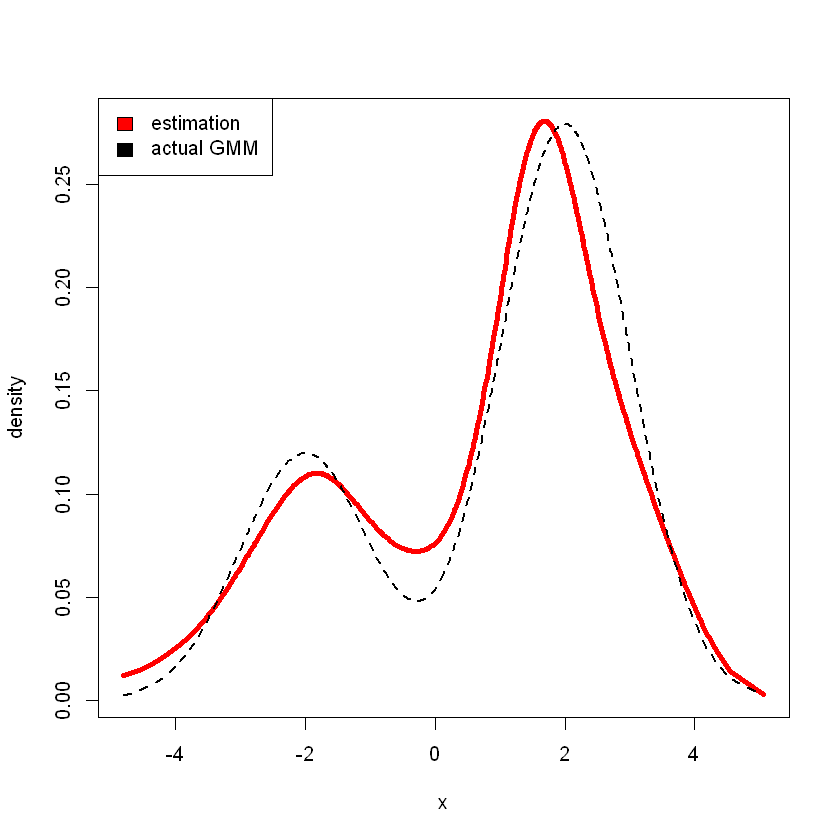
Consider sampling from GMM model

\[0.7N(2,1) + 0.3N(-2, 1)\]
# randomly sample 500 points from given GMM
x <- ifelse(runif(500) < .7, rnorm(500, 2, 1), rnorm(500, -2, 1))
# estimate density using p = 8
r <- den.splines(x,p=8)
# estimation
plot(r$x,r$density,type="l",xlab="x",ylab="density",lwd=4,col="red")
# actual
lines(r$x,0.3*dnorm(r$x,-2,1)+0.7*dnorm(r$x,2,1),lwd=2,lty=2)
legend("topleft", c("estimation", "actual GMM"), fill=c("red", "black"))

​

png

Hazard Functions

For \(X\) is a positive continuous rv, its hazard function is

\[h(x) = \frac{f(x)}{1-F(x)}\]

The motivation behind is to consider \(X\) as the survival time, consider

\[\begin{align*} \delta^{-1}P(x<X<x+\delta\mid X>x) &= \delta^{-1}\frac{P(x<X\leq x+\delta)}{P(X>x)}\\ &= \delta^{-1}\frac{F(x+\delta) - F(x)}{1-F(x)}\\ &\rightarrow_{\delta\rightarrow 0} \frac{f(x)}{1-F(x)} =:h(x) \end{align*}\]

Therefore, this represents instantaneous death rate given survival to time \(x\).

Also, note that

\[h(x) = \frac{f(x)}{1-F(x)} = -\frac{d}{dx}\ln(1-F(x))\]

Therefore,

\[F(x) = 1 - \exp(-\int_0^x h(t)dt), f(x) = h(x)\exp(-\int_0^x h(t)dt)\]

In this case, we require \(\int_0^\infty h(x)dx = \infty\) so that to have a "proper" probability distribution.

The shape of the hazard function gives info not immediately apparent in \(f\) or \(F\). \(h(x)\) increasing indicates new better than used, decreasing indicates used better than new