Density Estimation
Histograms
Given data \(x_1,...,x_n\) and "bins" \(B_k = [u_{k-1}, u_k), k=1,...,m\), then
Note that \(\text{hist}\) is a pdf since \(\text{hist}(x)\geq 0\) and
Histogram depends on number of bins and boundaries of the bins.
Substitution principle estimation
Consider the empirical distribution function
However, we cannot derive any \(f\) since this is not differentiable.
Kernel Density estimation
Start with a density function \(w(x)\), i.e. a kernel
Given \(w\) and a bandwidth \(h\), define the kernel density estimator
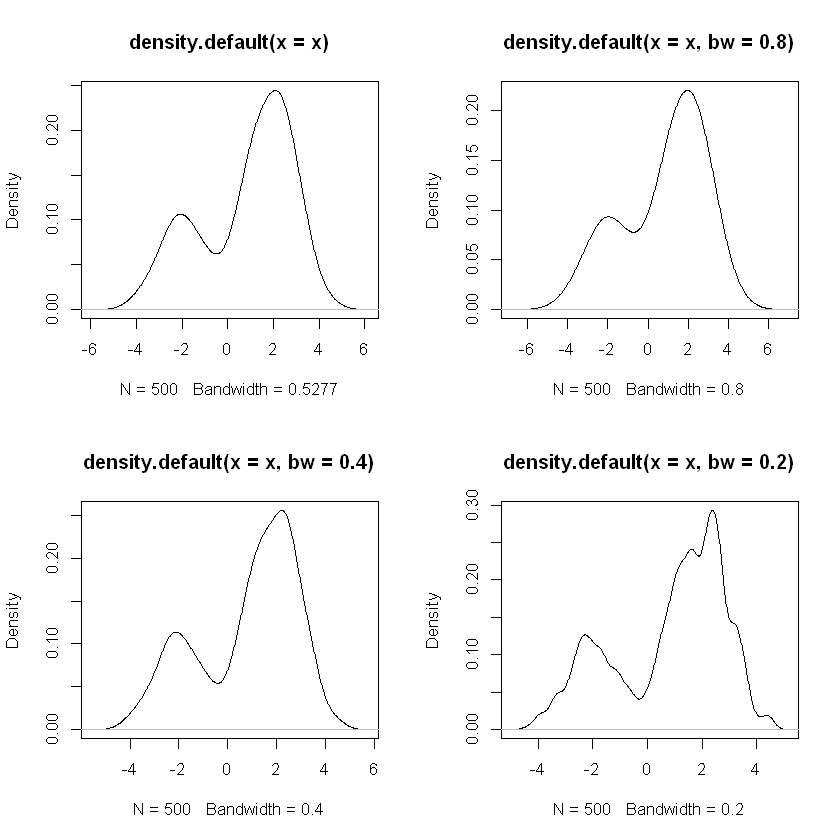
bandwidth controls the amount of smoothing, as \(h\) increases, the estimator \(\hat f_h(x)\) becomes smoother.
Some examples of kernels are
- Gaussian kernel \(w(x) = \sqrt{2\pi}^{-1}\exp(\frac{-x^2}{2})\)
- Epanechinkov kernel \(w(x) = \frac{3}{4\sqrt 5}(1-\frac{x^2}{5}), |x|\leq \sqrt 5\)
- Rectangular \(w(x) = \frac{1}{2\sqrt{3}}, |x| \leq \sqrt 3\)
- Triangular \(w(x) = \frac{1}{\sqrt 6}(1-\frac{|x|}{\sqrt 6}), |x|\leq \sqrt 6\)
Example
Draw 500 observations from
N <- 500
components <- sample(1:2,prob=c(.7, .3),size=N,replace=TRUE)
mus <- c(2, -2)
x <- rnorm(n=N,mean=mus[components],sd=1)
par(mfrow=c(2, 2))
.5387 - plot(density(x))
.8 - plot(density(x, bw=.8))
.4 - plot(density(x, bw=.4))
.2 - plot(density(x, bw=.2))
Redistribution
The empirical distribution function \(\hat F\) puts probability mass \(1/n\) at each of the points \(X_1,...,X_n\), use the kernel with bandwidth \(h\) to redistribute this mass around each \(X_i\), probability density around \(X_i = \frac{1}{nh}w(\frac{x-X_i}{h})\) where
The density estimate is now simply the sum of these densities over all observations
Convolution
Look at the distribution of \(Y_h = U+hV\) where \(U\sim \hat F\) and \(V\) has density \(w\) with \(V,U\) independent. If \(h\) is small then \(Y_h \approx U \sim \hat F\).
Unlike \(U, Y_h\) is a continuous r.v. for each \(h>0\):
Choice of bandwidth
The choice of \(h\) depends on what we believe the underlying density looks like, if \(f\) is believed to be smooth, then take larger \(h\). If \(f\) is believed to have a number of modes (i.e. local maxima) then we should take smaller \(h\).
Consider the bias-variance decomposition
As \(h\) decreases, the squared bias term also decrease but the variance increases.
Example: The rectangular kernel
Take \(w(x) = 1/2\) for \(|x|\leq 1\). Then,
The mean of \(\hat{f_h}(x)\) is
the squared bias is
For the variance,
Thus, we can approximate the variance by
The MSE is approximately
Uncertainty Estimating
Let \((X_1,..., X_n)\sim F_\theta\) for some \(\theta \in \Theta \subset R\), want to estimate \(\theta\) using \(X_1,...,X_n\).
Let \(\hat\theta\) be the estimator of the true \(\theta\), but we don't know what \(\theta\) is, so how can we say about the estimation error?
Example
Let \(X_1,...,X_n\) indep. \(N(\mu, \sigma^2)\) random variables. Estimate \(\mu = E(X_i)\) by \(\hat\mu = \bar X\) (substitution principle estimator).
We know that \(\hat\mu \sim N(\mu, \sigma^2/n)\). Then
In this example, knowing the distribution of \(\hat\mu\) tells us a lot about the uncertainty of \(\hat\mu\) of an estimator of \(\mu\).
If \(\sigma^2\) is unknown then we can estimate
and replace 1.96 by some \(t\).
Sampling distribution of \(\hat\theta\) is its probability distribution; this will depend on \(\theta\).
Mean square error of \(\hat\theta\) is defined as
Unbiased if \(bias_\theta(\hat \theta) := E_\theta(\hat\theta) - \theta = 0\)
Problem with unbiasedness
- In many problems, unbiased estimators do not exist
- In some problems, the estimator lies outside the parameter space with positive probability
- If \(\hat\theta\) is an unbiased estimator of \(\theta\) and \(g\) is a non-linear function then \(E_\theta[g(\hat\theta)] \neq g(\theta)\) unless \(P_\theta(\hat\theta = \theta) = 1\).
When to worry about bias?
- If \(\hat\theta\) is systematically larger or smaller than \(\theta\)
- If the squared bias is approximately equal to or greater than the variance
Example: Sample variance
\(X_1,...,X_n\) indep. with \(\mu, \sigma^2\), using unbiased estimator of sample variance
However, \(S = \sqrt{S^2}\) is biased, if we assume that \(X_1,...,X_n\) are Normal then we can evaluate the bias explicitly
Then
Consistency
The sequence of estimators \(\hat\theta_n\) is consistent for \(\theta\) if for each \(\epsilon > 0\) and \(\theta\in\Theta\),
a.k.a. \(\hat\theta_n \rightarrow^p \theta\)
Note that consistency is an aspirational property:
- if we have enough info. then we can estimate \(\theta\) arbitrarily precisely.
- For a finite \(n\), consistency isn't meaningful
Sample means and functions thereof
\(X_1,...,X_n\) indep. with mean \(\mu\) and \(\sigma^2\), then estimate \(\mu\) by \(\hat\mu_n = n^{-1}\sum_{i=1}^n X_i\)
By WLLN, \(\hat\mu_n\) is a consistent estimator of \(\mu\) (i.e. \(\{\hat\mu_u\}\) is consistent).
Likewise, if we want to estimate \(\theta = g(\mu)\) where \(g\) is a continuous function then \(\hat\theta_n = g(\hat\mu_n)\) is a consistent estimator of \(\theta\).
We can also approximate the sampling distributions of \(\hat\mu_n\) and \(\hat\theta_n\) by normal distributions
Example: Regression design
Assume for simplicity that \(\epsilon_1,...,\epsilon_n\) are indep. \(N(0,\sigma^2)\)
Least squares estimator of \(\beta_1\):
Thus \(\hat\beta_1 = \hat\beta_1^{(n)}\) will be consistent provided that
Sampling distributions and standard errors
Assume \(\hat\theta\) is an estimator of some parameter \(\theta\), then \(se(\hat\theta)\) is defined to be the standard deviation of the sampling deviation of the sampling distribution of \(\hat\theta\).
This is rarely known exactly but can usually be approximated somehow.
If \(\hat\mu = \bar X\) where \(\bar X\) is based on \(n\) indep. observations with variance \(\sigma^2\) then \(se(\hat\mu) = \sigma/\sqrt n\).
If the sampling distribution is approximately normal then we can approximate the standard error by the standard deviation of the approximating normal distribution.
Example
\(\hat\mu = \bar X, se(\hat\mu) = \sigma/\sqrt n\). estimated standard error is
Example: the Delta Method estimator
\(X_1,...,X_n\) indep. with some unknown cdf \(F\), suppose \(\hat\theta = g(\bar X)\).
If \(g\) is differentiable then we can approximate the sampling distribution of \(\hat\theta\) by a normal distribution using Delta Method:
where \(\sigma^2 = var(X_i)\) This suggests that we can estimate \(se(\hat\theta)\) using the Delta Method estimator
where \(S^2\) is the sample variance of \(X_1,...,X_n\).
We are using the substitution principle here to estimate the unknown \(\mu\) and \(\sigma^2\)
Recall that the Delta Method follows from the Taylor series approximation
Thus
We "estimate" \(\phi(X_i)\) by a pseudo-value
Note that
The Delta Method estimator can now be written as
Example: Trimmed mean
\(X_1,...,X_n\) indep. continuous r.v. with density \(f(x-\theta)\) where \(f(x) = f(-x)\) and \(\theta\) is unknown. if suspecting that \(f\) is heavy-tailed, then we want to eliminate the effects of extreme observations.
To minimize the effect of extreme observations, we estimate \(\theta\) by a trimmed mean:
In general, the trimmed mean is a substitution principle estimator of
where \(a = r/n\).
Then, the sampling distribution of trimmed mean is approximately normal
where
Approximating estimators by sample means
Suppose that \(\hat\theta\) is some complicated estimator like a trimmed mean.
How to compute \(\hat{se}(\hat\theta)\), suppose that we can approximate \(\hat\theta\) by an average \(\hat\theta \approx n^{-1}\sum^n \phi(X_i)\)
This suggests using
where \(\bar\phi = \frac1n \sum^n \phi(X_i)\approx \hat\theta\)
Leave-one-out estimators
Suppose that \(\hat\theta = \hat\theta(X_1,...,X_n)\), then define \(\hat\theta_{-i} = \hat\theta(X_1,...,X_{i-1}, X_{i+1},...,X_n)\)
if \(\hat\theta = \bar X\) then \(\hat \theta_{-i} = \frac1{n-1}\sum_{j\neq i}X_j\)
Example: Theil Index
Define \(\theta(F) = E_F[\frac{X_i}{\mu(F)}\ln (\frac{X_i}{\mu(F)})]\) where \(P(X_i > 0) = 1\) and \(\mu(F) = E_F(X_i)\).
We estimate \(\theta(F)\) by
The leave-one-out estimators are
where \(\bar X_{-i} = \frac1{n-1}\sum_{j\neq i}X_j\)
From leave-one-out to pseudo-values
Suppose that we can approximate \(\hat\theta\) by a sample mean
for some (unknown) function \(\phi\).
Then for the leave-one-out estimators, we have
This suggests that we can recover \(\phi(X_i)\) (approximately) by the pseudo-value
The pseudo-values can be used to estimate the s.e. of \(\hat\theta\).
Jackknife s.e. estimator
Given the pseudo-values \(\Phi_1,...,\Phi_n\), define the jackknife estimator of \(se(\hat\theta)\)
where \(\hat\theta_\cdot = \frac1n \sum^n \hat\theta_{-i}\)
For many estimators, we have
We can use the jacknife to remove the \(1/n\) bias term.
Define the bias-corrected \(\hat\theta\):
For \(\hat\theta_{bc}\), then
x <- rgamma(100,2)
y <- x/mean(x)
theil <- mean(y*log(y))
sprintf("theil index %f", theil)
# Compute pseudo-values
pseud <- NULL
for (i in 1:100) {
xi <- x[-i]
yi <- xi/mean(xi)
loo <- mean(yi*log(yi))
pseud <- c(pseud,100*theil - 99*loo)
}
sprintf("mean of pseudo %f", mean(pseud)) # mean of pseudo-values - bias-corrected estimate
sprintf("jackknife s.e. estimate %f", sqrt(var(pseud)/100))
theil index 0.188827
mean of pseudo 0.190167
jackknife s.e. estimate 0.022019
Delta Method vs. Jackknife
Sample 100 observations from a Gamma distribution with \(\alpha = 2\) and \(\lambda = 1\).
Estimate \(\theta = \ln(\mu) = g(\mu); g'(\mu) = 1/\mu\). For our sample \(\bar x = 1.891\) and \(s^2 = 1.911\), \(\hat \theta = \ln(\bar x) = 0.637\)
Thus the Delta Method s.e. estimate is
Computing the jackknife estimate is somewhat more computationally intensive.
x <- rgamma(100,2)
thetaloo <- NULL
for (i in 1:100) {
xi <- x[-i]
thetaloo <- c(thetaloo,log(mean(xi)))
}
jackse <- sqrt(99*sum((thetaloo-mean(thetaloo))^2)/100)
sprintf("jackkniefe s.e. %f", jackse)
jackkniefe s.e. 0.070312
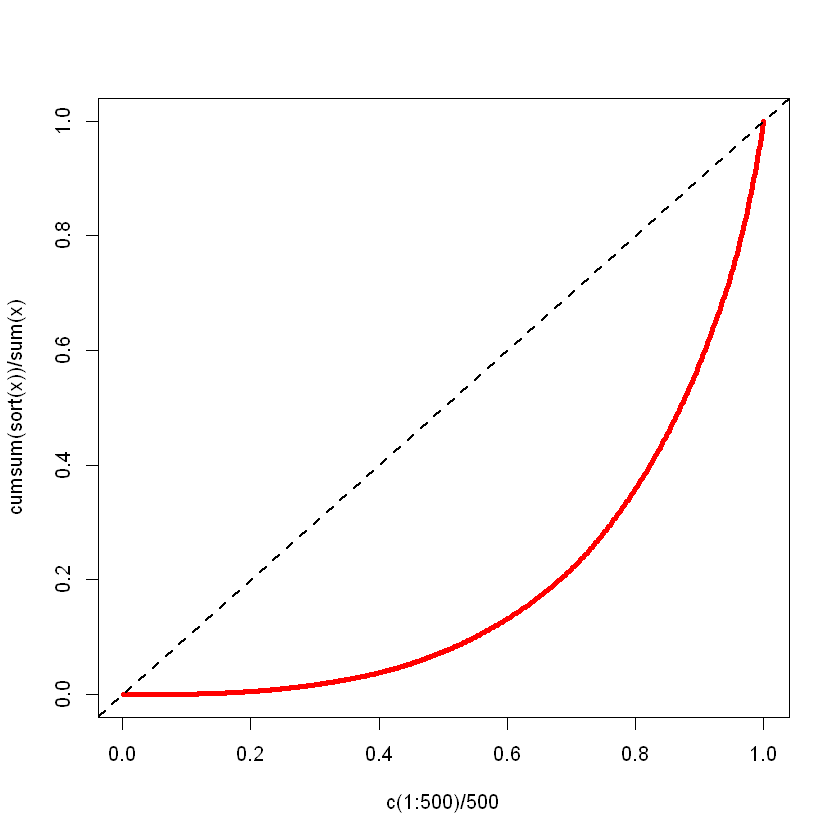
Example: The Lorenz curve
Suppose that \(F\) is the cdf of a positive r.v. with finite mean \(\mu(F)\), let \(F\) describes the income distribution within some population.
For each such \(F\), we can define its Lorenz curve:
a.k.a. the fraction of total income held by poorest \(\tau\).
\(\mathcal L_F(\tau) \leq \tau\) with \(\mathcal L_F(0) = 0\) and \(\mathcal L_F(1)=1\).
The difference between \(\tau\) and \(\mathcal L_F(\tau)\) can be used to measure income inequality.
Example: The Gini index
One measure of income inequality is the Gini index defined by
\(Gini(F)\in [0,1]\Rightarrow 0\) perfect equality, \(1\) perfect inequality.
We estimate the quantiles \(F^{-1}(\tau)\) by order statistics. Given indep. observations \(X_1,...,X_n\) from \(F\), we have
gini <- function(x) {
# compute point estimate
n <- length(x)
x <- sort(x)
wt <- (2*c(1:n)-1)/n - 1
g <- sum(wt*x)/sum(x)
# compute leave-one-out estimates
wt1 <- (2*c(1:(n-1))-1)/(n-1) - 1
gi <- NULL
for (i in 1:n) {
x1 <- x[-i] # data with x[i] deleted
gi <- c(gi,sum(wt1*x1)/sum(x1))
}
# compute jackknife std error estimate
gbar <- mean(gi)
se <- sqrt((n-1)*sum((gi-gbar)^2)/n)
r <- list(gini=g,se=se)
}
# generate 500 observations from a Gamma( a = 1/2 )
x <- rgamma(500,1/2) # Sample from a Gamma with alpha=1/2
r <- gini(x)
sprintf("gini %f", r$gini)
sprintf("s.e. %f", r$se)
gini 0.626679
s.e. 0.012652