Multi Comparisons and One Way ANOVA

Multiple Comparisons

post hoc procedure: further comparisons after significant result from overall One-way ANOVA
If the result for One-way ANOVA is good enough, i.e.some pairs are evidently true, we may omit some pairs to remove the number of tests
Max of \(G \choose 2\) pairwise comparisons
Major issue: increased chance of making at least one Type I error when carrying out many tests, \(E(\#errors)=\#tests \times \alpha\)
Two common solutions: based on controlling family Type I error rate, choose
- Bonferroni
- Tukey's

Example \(P(\text{committing at least 1 Type I error})\) ?

For n independent tests: \(P = 1-(1-\alpha)^n\)

Bonferroni's Method

Based on Bonferroni's inequality \(P(A\cup B) \leq P(A)+P(B)\), hence \(P(\cup A_i)\leq \sum P(A_i), A_i:=\) the event that \(i\)th test results in a Type I error.
Method: conduct each of \(k=G \choose 2\) pairwise tests at level \(\alpha / k\)
CI: \(|\bar{y}_i - \bar{y}_j|\pm t_{\alpha/2k} S_p \sqrt{n_i^{-1} + n_j^{-1}}\)
Conservative: overall Type I error rate is usually much less than \(\alpha\) if tests are not mutually independent.
Type II error inflation.

Tukey's Approach

Usually less conservative than Bonferroni, particularly if group sample size are similar. Controls the overall Type I error rate of \(\alpha\), simultaneous CI converage rate is \(1-\alpha\).

Studentized Range distribution

\(\mathcal{X}= \{X_1,...,X_n\}, X_i\in N(\mu,\sigma^2)\). Determine the distribution of the max and min of \(\mathcal{X}\).
\(X_{(n)}:=\max{\mathcal{X}}, X_{(1)};=\min{\mathcal{X}}\), Range \(:= X_{(n)}-X{(1)}\)
Based on \(n\) observations from \(X\), the Studentized range statistic is \(Q_{stat} = Range / s, s=\) sample std.
Based on \(G\) group means, with \(n\) observations per group:

\[\bar{Q}_g = \frac{\sqrt{n}(\bar{y}_{(g)} - \bar{y}_{(1)})}{s_v}\]

\(s_v\) estimator of the pooled std. \(v=N-G=G(n-1)\) d.f.

If there are \(G\) groups, then there is a max of \(k\) pairwise differences
Controlling overall simultaneous Type I error rate v.s. Individual Type I error rate
Find a pairwise significant difference
- Compare method-wise significant difference, \(c(\alpha)\) with \(|\bar{y}_i - \bar{y}_j|\) OR
- determine whether CI contains 0 OR
- Compare \(p\) with \(\alpha\)
\(s=\sqrt{MSE}\) with d.f. \(=v=d.f.Error\)

Tukey's Honestly Significant Difference (HSD)

let \(q(G,v,\alpha)/t^*:=\) the critical value from the Studentized Range distribution.
Family rate \(=\alpha\)
Tukey's HSD \(=q(G,v,\alpha) \frac{s}{\sqrt{n}}\)

Case Study

Bonferroni

\(H_0:\mu_i - \mu_j = 0, H_a: \mu_i\neq \mu_j\)
\(t = \frac{\bar{x}_i - \bar{x}_j}{S_p \sqrt{n_i^{-1} + n_j^{-1}}}\)
\(p = 2P(T_{\alpha/2k}> |t|)\)

# import data
library(Sleuth2)
jury = case0502
percent = case0502$Percent
judge = case0502$Judge

judge = relevel(judge, ref="Spock's")
pairwise.t.test(percent, judge, p.adj='bonf')

    Pairwise comparisons using t tests with pooled SD

data:  percent and judge

  Spock's A       B       C       D       E      
A 0.00022 -       -       -       -       -      
B 0.00013 1.00000 -       -       -       -      
C 0.00150 1.00000 1.00000 -       -       -      
D 0.57777 1.00000 1.00000 1.00000 -       -      
E 0.03408 1.00000 1.00000 1.00000 1.00000 -      
F 0.01254 1.00000 1.00000 1.00000 1.00000 1.00000

P value adjustment method: bonferroni

# CI
lmod=lm(percent~judge)
confint(lmod, level = 1- 0.05/nlevels(judge))

A matrix: 7 × 2 of type dbl
	0.357 %	99.643 %
(Intercept)	8.078085	21.16636
judgeA	8.547341	30.44821
judgeB	8.647254	29.34163
judgeC	5.222969	23.73259
judgeD	-2.969585	27.72514
judgeE	1.997255	22.69163
judgeF	2.922970	21.43259

amod = aov(percent~judge)
hsd = TukeyHSD(amod, 'judge')
hsd

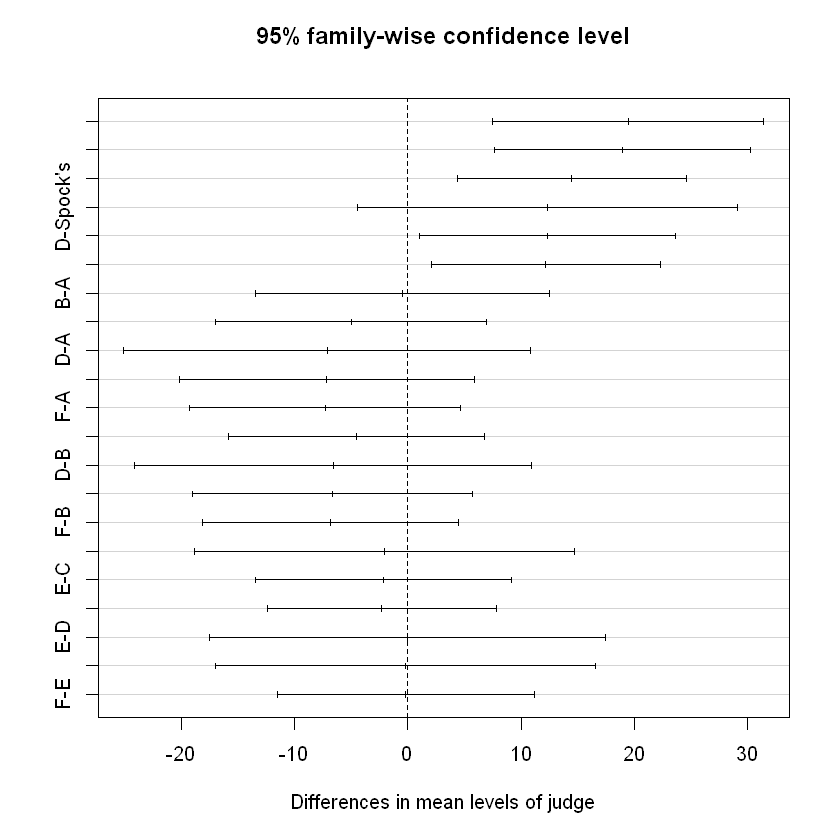
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = percent ~ judge)

$judge
                 diff        lwr       upr     p adj
A-Spock's 19.49777727   7.514685 31.480870 0.0001992
B-Spock's 18.99444405   7.671486 30.317402 0.0001224
C-Spock's 14.47777732   4.350216 24.605339 0.0012936
D-Spock's 12.37777758  -4.416883 29.172438 0.2744263
E-Spock's 12.34444443   1.021486 23.667402 0.0248789
F-Spock's 12.17777766   2.050216 22.305339 0.0098340
B-A       -0.50333322 -13.512422 12.505755 0.9999997
C-A       -5.01999995 -17.003092  6.963092 0.8470098
D-A       -7.11999969 -25.094638 10.854639 0.8777485
E-A       -7.15333284 -20.162421  5.855755 0.6146239
F-A       -7.31999961 -19.303092  4.663093 0.4936380
C-B       -4.51666673 -15.839625  6.806291 0.8742030
D-B       -6.61666648 -24.158118 10.924785 0.9003280
E-B       -6.64999962 -19.053679  5.753679 0.6418003
F-B       -6.81666639 -18.139624  4.506292 0.5109582
D-C       -2.09999975 -18.894661 14.694661 0.9996956
E-C       -2.13333289 -13.456291  9.189625 0.9968973
F-C       -2.29999966 -12.427561  7.827562 0.9914731
E-D       -0.03333314 -17.574784 17.508118 1.0000000
F-D       -0.19999992 -16.994661 16.594661 1.0000000
F-E       -0.16666677 -11.489625 11.156291 1.0000000

plot(hsd)

Linear Regression Model

\(Y_{N\times 1}=X_{N\times(p+1)}\beta_{(p+1)\times 1} + \epsilon_{N\times 1}\), response \(Y\) continuous, explanatory \(X\) categorical and/or continuous
\(Y\) is linear in the \(\beta\)'s i.e. no predictor is a linear function or combination of other predictors
\(\hat{\beta}=(X'X)^{-1}X'Y\) Least square Estimate, need\(rank(X'X)=rank(X)\Rightarrow\) columns of \(X\) must be linear independent
Null hypothesis \(H_0: \beta = \vec{0}\). Assumptions
Appropriate Linear Model
Uncorrelated Errors
\(\vec{\epsilon}\sim N(\vec{0},\sigma^2I)\).
Sum of Squares Decomposition

\[\begin{align*}SST&=SSE+SSR\\ \sum_i^N(Y_i-\bar{Y})^2 &= \sum_i^N (Y_i-\hat{Y}_i)^2 + \sum_i^N(\hat{Y}_i - \bar{Y})^2 \end{align*}\]

One-Way ANOVA

Need one factor (categorical variable) with at least 2 levels \((G\geq 2)\)
Aim: Compare \(G\) group means

\[H_0:\mu_1=\mu_2=...=\mu_G, H_a:\exists i\neq j. \mu_i\neq \mu_j\]
Predictors are indicator variables that classify the observations one way (into \(G\) groups)
- special case of a general linear model
- equivalent to GLM with one-way classification (one factor)
- GLM uses \(G-1\) dummy variables
ANOVA: compare means by analyzing variability

One Way Expectations and Estimates

\[\begin{align*} E(Y_i)&=(\beta_0 + \beta_1,...,\beta_0 +\beta_{G-1}, \beta_0)^T\\ \hat{Y}_i &= (b_0+b_1,...,b_0 + b_{G-1}, b_0)^T\\ \hat{\beta} &= (b_0,...,b_{G-1})^T = (\bar{y}_G, \bar{y}_1-\bar{y}_G,...,\bar{y}_{G-1}-\bar{y}_G)^T \end{align*}\]

Then, the null hypothesis is \(H_0: \beta_i=\mu_i-\mu_0 = 0\Rightarrow\) the equal mean of \(i\)th group and the compared group

In this case, for \(SST\), \(N=\sum_1^G n_i,\hat{Y}_i=\) mean of observations for group \(g\) from which the \(i\)th observation belongs, \(\bar{Y}=\frac{\sum_{g=1}^{G}\sum_{j=1}^{n_g} y_{gj}}{N}\) is the grand mean

\[\begin{align*} SSReg &= \sum_{g=1}^G n_g(\bar{Y}_g-\bar{Y})^2\\ RSS &= \sum_{g=1}^G \sum_{g} (Y_i-\bar{Y}_g)^2 \end{align*}\]

# import data
library(Sleuth2)
jury = case0502
percent = case0502$Percent
judge = case0502$Judge

table(judge)

judge
Spock's       A       B       C       D       E       F 
      9       5       6       9       2       6       9

with(jury, tapply(percent, judge, mean))

Spock's     14.6222224235535
A           34.1199996948242
B           33.6166664759318
C           29.0999997456868
D           27
E           26.9666668574015
F           26.800000084771

Compare 6 judges (exclude Spock)

others = subset(jury, judge != "Spock's") 
boxplot(others$Percent~others$Judge, data=others)

summary(aov(others$Percent~others$Judge))

             Df Sum Sq Mean Sq F value Pr(>F)
others$Judge  5  326.5   65.29   1.218  0.324
Residuals    31 1661.3   53.59

Rule of thumb

Not a formal way, not a quick check whether equal variance

sss <- with(others, tapply(others$Percent, others$Judge, sd))
sss

Spock's     <NA>
A           11.9418181005452
B           6.58222301297842
C           4.59292918339244
D           3.81837769736668
E           9.01014223675898
F           5.96887758208529

max(sss, na.rm=T); min(sss, na.rm=T)

11.9418181005452
3.81837769736668

max(sss, na.rm=T) / min(sss, na.rm=T) > 2

TRUE

bartlett.test(others$Percent, others$Judge)

    Bartlett test of homogeneity of variances

data:  others$Percent and others$Judge
Bartlett's K-squared = 6.3125, df = 5, p-value = 0.277

The small p-value may due to the uneven and small group sizes

Compare all 7 judges

boxplot(percent~judge)

summary(aov(percent~judge))

            Df Sum Sq Mean Sq F value  Pr(>F)    
judge        6   1927   321.2   6.718 6.1e-05 ***
Residuals   39   1864    47.8                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

summary(lm(percent~judge))

Call:
lm(formula = percent ~ judge)

Residuals:
    Min      1Q  Median      3Q     Max 
-17.320  -4.367  -0.250   3.319  14.780

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   14.622      2.305   6.344 1.72e-07 ***
judgeA        19.498      3.857   5.056 1.05e-05 ***
judgeB        18.994      3.644   5.212 6.39e-06 ***
judgeC        14.478      3.259   4.442 7.15e-05 ***
judgeD        12.378      5.405   2.290 0.027513 *  
judgeE        12.344      3.644   3.388 0.001623 ** 
judgeF        12.178      3.259   3.736 0.000597 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.914 on 39 degrees of freedom
Multiple R-squared:  0.5083,    Adjusted R-squared:  0.4326 
F-statistic: 6.718 on 6 and 39 DF,  p-value: 6.096e-05

par(mfrow=c(2,2))
plot(lm(percent~judge))

ssa = with(jury, tapply(percent,judge,sd))
ssa

Spock's     5.03879411343757
A           11.9418181005452
B           6.58222301297842
C           4.59292918339244
D           3.81837769736668
E           9.01014223675898
F           5.96887758208529

max(ssa) / min(ssa) > 2

TRUE

bartlett.test(percent~judge)

    Bartlett test of homogeneity of variances

data:  percent by judge
Bartlett's K-squared = 7.7582, df = 6, p-value = 0.2564

Residual vs Fitted: No obvious pattern, assume equal variance (also by rule of thumb and Bartlett)
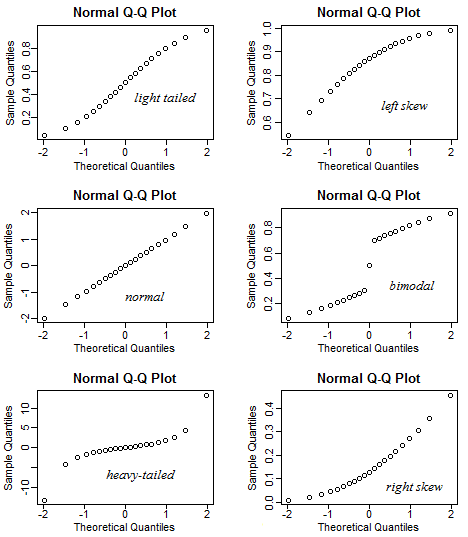
Normal Q-Q: overall OK
Outliers: see Residual vs leverage, not influential point.