AWS Trainium and NKI kernel
Based on Stanford CS149 Assignment, NKI kernel Docs
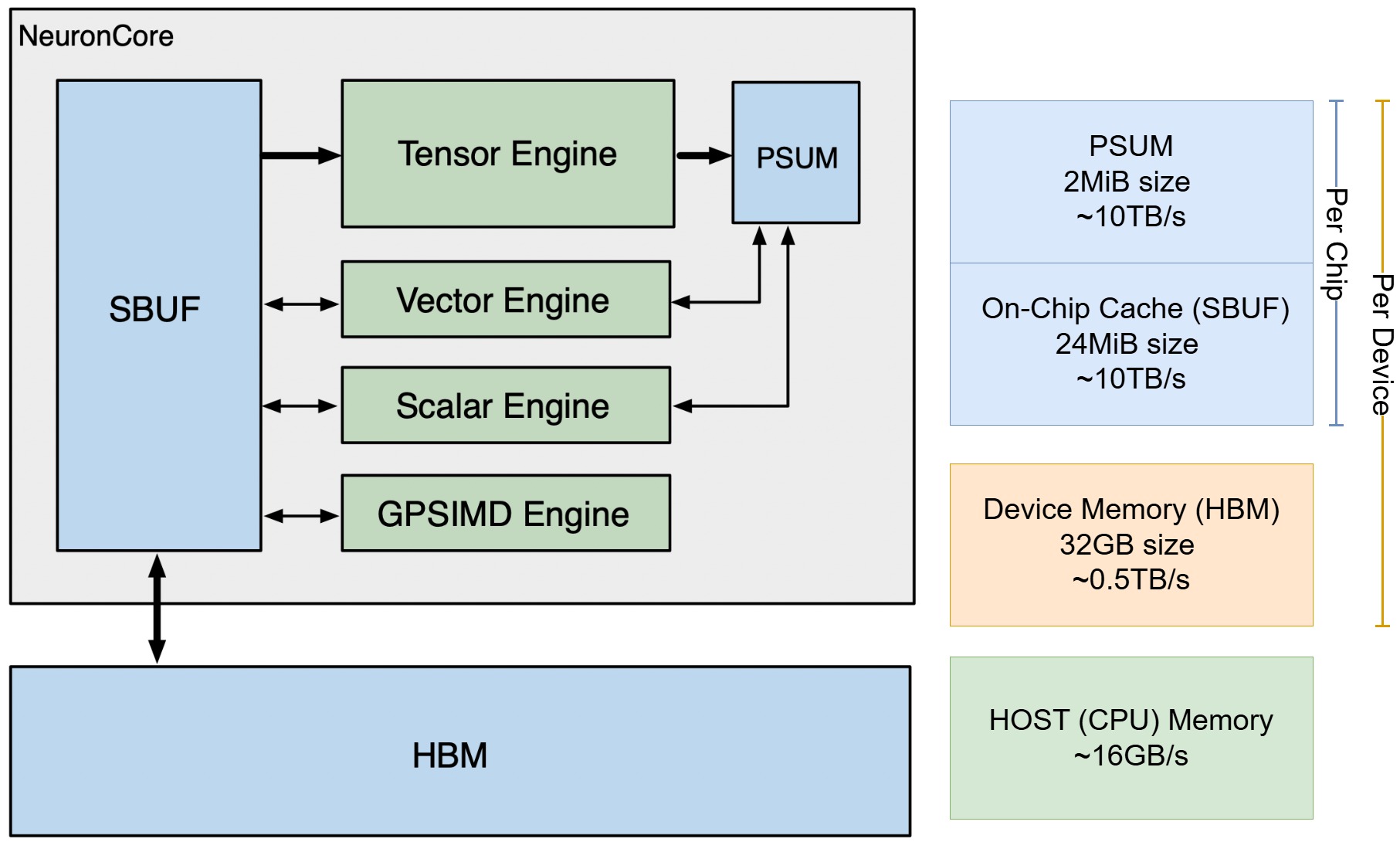
Trainium Hardware Architecture
- HBM: High bandwidth memory, device memory. Host to device should be managed by ML framework or external of NKI kernel.
- SBUF: State buffer. Software-managed on-chip SRAM. In NKI programming, on-chip SRAM is not a hardware managerd "cache", HBM to SBUF needs explicit
loadandstore. - PSUM: Partial Sum Buffer, a small, dedicated memory designed for storing matrix multiplication results.
- Tensor Engine: for matmuls, or other operators that can be executed as matmuls. The engine has 128x128 systolic processing elements, which streams input data from SBUF and write output to PSUM.
- Vector Engine: for vector operations that depends on multiple elements from input tensors (vector reduction, element-wise binary operations). VectorE consists of 128 parallel vector lanes.
- Scaler Engine: for element-wise operations, where every element in the output tensor only depends on one element of the input tensor. Usually used for hardware-accelerated activation functions. ScalarE consists of 128 parallel vector lanes.
- GpSimd Engine: for general SIMD operations. Basically a 8-core CPU, with 512-bit vector machine.
Systolic Arrays
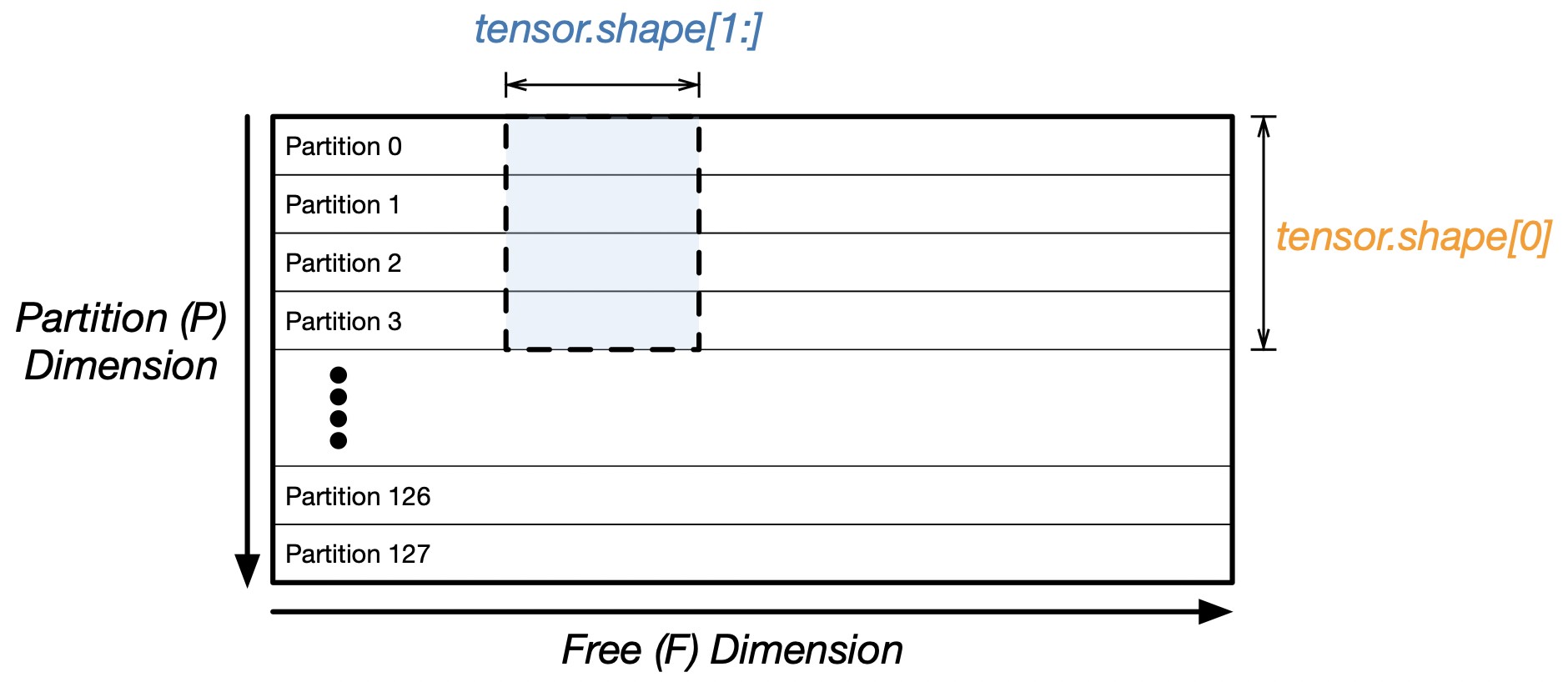
Trainium chips are operated in systolic arrays, hence all data movements and computations are tiled. From the hardware perspective, the on-chip memories, SBUF and PSUM, are arranged as 2D memory arrays. The first dimension is the partition dimension P with nki.tile_size.pmax = 128 memory partitions that can be read and written in parallel by compute engines. The second dimension is the free dimension F where elements are read and written sequentially.
PSUM Constraints
Remind that PSUM is the small, dedicated on-chip memory for matmul reduction operations. Currently, its size is 2MiB. The hardware design poses a constraint for tiles in PSUM, nki.tile_size.psum_fmax == 512, which comes from 2MiB / 128 / 32B.
For matrix multiplicaion of size \((M, K) \times (K, N)\). The contraction dimension \(K\) consider how matrix is mapped onto tensorE and PSUM. We define that input tiles F dimension size must not exceed M_per_tile = nki.tile_size.gemm_stationary_fmax == 128 on the left-hand side (LHS), or N_per_tile = nki.tile_size.gemm_moving_fmax == 512 on the right hand size (RHS). More explanation in Tensor Engine: Matrix Multiplication.
NKI (Neuron Kernel Interface)
NKI kernels are written in Python. Essentially, NKI programming and some optimization considerations are
-
Loading data from HBM to on-chip SBUF
- How to minimize the data movement.
- How to do data tiling so that we can fully use the 128 lane.
-
Computations on the compute engines
- How to overlap computations on different cores.
-
Storing outputs from SBUF back to HBM
Each NKI kernel is a python function decorated with @nki.jit, and the arguments should be tensors already reside in HBM. NKI kernels can be directly inserted into ML frameworks (PyTorch, Tensorflow).
@nki.jit
def vector_add(a_vec: Tensor, b_vec: Tensor) -> Tensor:
# Allocate space for the output vector in HBM
out = nl.ndarray(shape=a_vec.shape, dtype=a_vec.dtype, buffer=nl.hbm)
# Load the input vectors from HBM into variables stored in SBUF
a = nl.load(a_vec)
b = nl.load(b_vec)
# Add the input vectors
res = nl.add(a, b)
# Store the result into HBM
nl.store(out, value=res)
return out
NKI provides a nki.baremetal decorator function to directly run kernels from numpy arrays.
vec_size = nki.tile_size.pmax # 128
a = np.random.rand(vec_size, dtype=np.float32)
b = np.random.rand(vec_size, dtype=np.float32)
out = nki.baremetal(vector_add)(a, b)
Data Tiling
The on-chip memories, SBUF and PSUM, store data that is arranged as 2D memory arrays. The first dimension of the 2D array is called the "partition dimension" P. The second dimension is referred to as the "free dimension" F (more details later). For vector add, we have P = vec_size, F = 1
Partition Dimension
Note that if we run the above code with vec_size > 128, we get
> a = nl.load(a_vec)
Value Error: number of partition in src[12800, 1] of 'load'
exceed architecture limitation of 128.
NeuronCores loads 128 elements in parallel along the P-dim in each cycle, which means the max size of P dimension for each nl.load is 128. Therefore, we need to manually tile of data into 128 chunks.
@nki.jit
def vector_add_tiled(a_vec, b_vec):
CHUNK_SIZE = nki.tile_size.pmax # 128
out = nl.ndarray(shape=a_vec.shape, dtype=a_vec.dtype, buffer=nl.hbm)
M = a_vec.shape[0]
# nl.affine_range assumes there are no loop-carried dependencies
# and allow more aggressive optimizations for the compiler pipelining
for m in nl.affine_range((M // ROW_CHUNK)):
# Allocate row-chunk sized tiles for the input vectors
a_tile = nl.ndarray((CHUNK_SIZE, 1), dtype=a_vec.dtype, buffer=nl.sbuf)
b_tile = nl.ndarray((CHUNK_SIZE, 1), dtype=b_vec.dtype, buffer=nl.sbuf)
# Load a chunk of rows
a_tile[...] = nl.load(a_vec[m * CHUNK_SIZE : (m + 1) * CHUNK_SIZE])
b_tile[...] = nl.load(b_vec[m * CHUNK_SIZE : (m + 1) * CHUNK_SIZE])
res = nl.add(a_tile, b_tile)
nl.store(out[m * CHUNK_SIZE : (m + 1) * CHUNK_SIZE], value=res)
return out
Free Dimension
The compiler is responsible the store and load are converted into direct memory access (DMA) instructions. Similar to how CUDA hides the data loading to threads, NeuronCore has 16 DMA engines to move multiple lanes of data in parallel / in pipeline. DMA are parallelized over the free dimension. In addition, the computation engines support pipelining over the free dimension.
@nki.jit
def vector_add_stream(a_vec, b_vec):
# The maximum size of our Partition Dimension
PARTITION_DIM = nki.tile_size.pmax # 128
# Free dim is a tunable parameter, and it depends on
# compiler optimizations/hardware specifications
FREE_DIM = 200
# The total size of each tile
TILE_M = PARTITION_DIM * FREE_DIM
# Get the total number of vector rows
M = a_vec.shape[0]
# Reshape the the input vectors
a_vec_re = a_vec.reshape((M // TILE_M, PARTITION_DIM, FREE_DIM))
b_vec_re = b_vec.reshape((M // TILE_M, PARTITION_DIM, FREE_DIM))
# Allocate space for the reshaped output vector in HBM
out = nl.ndarray(shape=a_vec_re.shape, dtype=a_vec_re.dtype, buffer=nl.hbm)
# Loop over the total number of tiles
for m in nl.affine_range((M // TILE_M)):
# Allocate space for a reshaped tile
a_tile = nl.ndarray((PARTITION_DIM, FREE_DIM), dtype=a_vec.dtype, buffer=nl.sbuf)
b_tile = nl.ndarray((PARTITION_DIM, FREE_DIM), dtype=a_vec.dtype, buffer=nl.sbuf)
# Load the input tiles
a_tile = nl.load(a_vec_re[m])
b_tile = nl.load(b_vec_re[m])
# Add the tiles together
res = nl.add(a_tile, b_tile)
# Store the result tile into HBM
nl.store(out[m], value=res)
# Reshape the output vector into its original shape
out = out.reshape((M,))
return out
Data Movement and Computation
F-dim is a tunable parameter, each DMA transfer has an overhead. However, F-dim is not always a "bigger means better" thing. Choosing a smaller F-dim may allow a better pipelining. In this case, since add requires small computation cycles, smaller free-dim means more but quicker data movement, and allow for more overlapping between the engines. In practice, we need to profile and decide the dimension size to harness better performance.
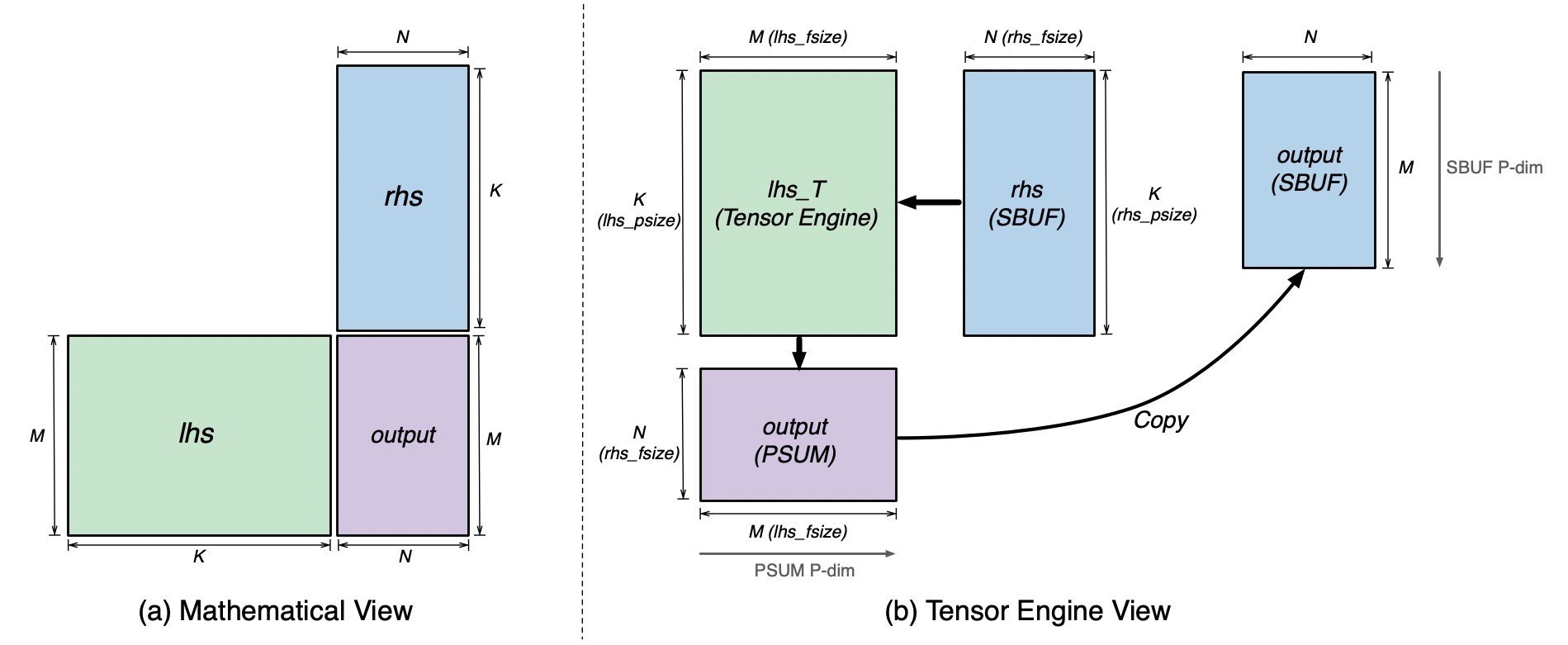
Tensor Engine: Matrix Multiplication
Consider the matmul, note that the hardware constrains that PSUM can only hold \(128\times 512\) elements. Thus, TILE_M = nki.tile_size.gemm_stationary_fmax == 128, TILE_N = nki.tile_size.gemm_moving_fmax == 512. In addition, the contraction dimension \(K\) has to be loaded in parallel and do element-wise multiplication, thus TILE_K = nki.tile_size.pmax = 128.
Similar to any parallel programming architecture, data locality (reducing data loading) is a key optimization. Check Matrix Multiplications notes. Reordering loop (nkm instead mnk to avoid reloading lhs elements) and blocked matmul apply to our case.
For trainium, SBUF is 24MiB. Assuming that we know the dtype and the rough shape of matrices (so that we can better choose number of tiles per block), we can compute the number of blocks s.t. data movement is minimized.
nki blocked matmul
import neuronxcc.nki as nki
import neuronxcc.nki.language as nl
import neuronxcc.nki.isa as nisa
@nki.jit
def nki_matmul_fully_optimized_(
lhsT,
rhs,
):
TILES_IN_BLOCK_M=16
TILES_IN_BLOCK_N=2
TILES_IN_BLOCK_K=8
K, M = lhsT.shape
K_, N = rhs.shape
assert K == K_, "lhsT and rhs must have the same contraction dimension"
result = nl.ndarray((M, N), dtype=lhsT.dtype, buffer=nl.shared_hbm)
TILE_M = nl.tile_size.gemm_stationary_fmax # 128
TILE_K = nl.tile_size.pmax # 128
TILE_N = nl.tile_size.gemm_moving_fmax # 512
BLOCK_M = TILE_M * TILES_IN_BLOCK_M
BLOCK_N = TILE_N * TILES_IN_BLOCK_N
BLOCK_K = TILE_K * TILES_IN_BLOCK_K
# the size has to be multiple of block size
# nl indexing cannot handle out of bound indexing
assert M % BLOCK_M == 0
assert N % BLOCK_N == 0
assert K % BLOCK_K == 0
NUM_BLOCK_M = M // BLOCK_M
NUM_BLOCK_N = N // BLOCK_N
NUM_BLOCK_K = K // BLOCK_K
# Blocking N dimension (the RHS free dimension)
for n in nl.affine_range(NUM_BLOCK_N):
result_tiles = nl.zeros((NUM_BLOCK_M, TILES_IN_BLOCK_M, TILES_IN_BLOCK_N,
nl.par_dim(TILE_M), TILE_N),
dtype=lhsT.dtype,
buffer=nl.sbuf)
# Blocking K dimension (the contraction dimension)
# Use `sequential_range` because we do not want the compiler to change this loop by,
# for example, vectorizing it
for k in nl.sequential_range(NUM_BLOCK_K):
# Loading tiles from rhs
# setting the load tile to `TILE_K x BLOCK_SIZE_N` to optimize DMA performance
i_rhs = nl.mgrid[0:TILE_K, 0:BLOCK_N]
rhs_tiles = nl.ndarray((TILES_IN_BLOCK_K, nl.par_dim(TILE_K), BLOCK_N),
dtype=rhs.dtype,
buffer=nl.sbuf)
for bk_r in nl.affine_range(TILES_IN_BLOCK_K):
rhs_tiles[bk_r, i_rhs.p, i_rhs.x] = nl.load(
rhs[(TILES_IN_BLOCK_K * k + bk_r) * TILE_K + i_rhs.p,
BLOCK_N * n + i_rhs.x])
# Blocking M dimension (the LHS free dimension)
for m in nl.affine_range(NUM_BLOCK_M):
# Loading tiles from lhsT
i_lhsT = nl.mgrid[0:TILE_K, 0:BLOCK_M]
lhsT_tiles = nl.ndarray((TILES_IN_BLOCK_K, nl.par_dim(TILE_K), BLOCK_M),
dtype=lhsT.dtype,
buffer=nl.sbuf)
for bk_l in nl.affine_range(TILES_IN_BLOCK_K):
lhsT_tiles[bk_l, i_lhsT.p, i_lhsT.x] = nl.load(
lhsT[(TILES_IN_BLOCK_K * k + bk_l) * TILE_K + i_lhsT.p,
BLOCK_M * m + i_lhsT.x])
# Do matmul with all tiles in the blocks
i_lhsT_mm = nl.mgrid[0:TILE_K, 0:TILE_M]
i_rhs_mm = nl.mgrid[0:TILE_K, 0:TILE_N]
i_res_mm = nl.mgrid[0:TILE_M, 0:TILE_N]
for bn in nl.affine_range(TILES_IN_BLOCK_N):
for bm in nl.affine_range(TILES_IN_BLOCK_M):
res_tile = nl.zeros((TILE_M, TILE_N), dtype=nl.float32, buffer=nl.psum)
for bk in nl.affine_range(TILES_IN_BLOCK_K):
res_tile[...] += nisa.nc_matmul(
lhsT_tiles[bk, i_lhsT_mm.p, bm * TILE_M + i_lhsT_mm.x],
rhs_tiles[bk, i_rhs_mm.p, bn * TILE_N + i_rhs_mm.x])
# Accumulate on corresponding SBUF tile
result_tiles[m, bm, bn, i_res_mm.p,
i_res_mm.x] += res_tile[i_res_mm.p, i_res_mm.x]
# Copying the result from SBUF to HBM
for m in nl.affine_range(NUM_BLOCK_M):
for bm in nl.affine_range(TILES_IN_BLOCK_M):
i_res = nl.mgrid[0:TILE_K, 0:TILE_N]
i_res_packed = nl.mgrid[0:TILE_K, 0:BLOCK_N]
result_packed = nl.ndarray((TILE_K, BLOCK_N),
dtype=result_tiles.dtype,
buffer=nl.sbuf)
# coalesce result tiles for better DMA performance
for bn in nl.affine_range(TILES_IN_BLOCK_N):
result_packed[i_res.p,
bn * TILE_N + i_res.x] = nl.copy(result_tiles[m, bm, bn,
i_res.p,
i_res.x])
nl.store(result[(TILES_IN_BLOCK_M * m + bm) * TILE_K + i_res_packed.p,
BLOCK_N * n + i_res_packed.x],
value=result_packed[i_res_packed.p, i_res_packed.x])
return result