Skip to content

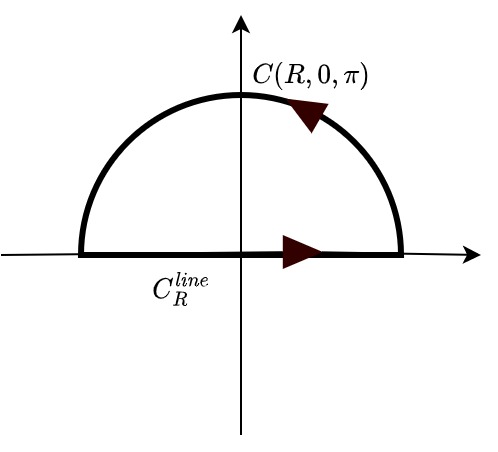
Jordon's Lemma

Claim 1

If zf(z)→unif.0zf(z)\rightarrow^{unif.} 0 as z→∞z\rightarrow\infty, then

lim⁡R→∞∫C(R,0,π)f(z)dz=0\lim_{R\rightarrow\infty} \int_{C(R,0,\pi)} f(z)dz = 0

where C(R,0,π)C(R,0,\pi) is the top semicircle arc of radius RR centered at 00, rotated ccw.

proof. Note that on the arc, ∣z∣=R|z| = R so that ∣zf(z)∣=R∣f(z)∣≤κ(R)|zf(z)| = R |f(z)| \leq \kappa(R) so that ∣f(z)∣≤κ(R)R|f(z)| \leq \frac{\kappa(R)}{R}.

Let ϵ>0\epsilon > 0. By definition of κ\kappa, take SS s.t. ∀R>S.κ(R)<ϵπ\forall R > S. \kappa(R) < \frac{\epsilon}{\pi}. Then, with ML inequality we have

∣∫C(R,0,π)f(z)dz∣≤πRκ(R)R<ϵ|\int_{C(R,0,\pi)} f(z)dz| \leq \pi R \frac{\kappa(R)}{R} < \epsilon

Example 1

Compute ∫−∞∞(x2+1)−1dx\int_{-\infty}^{\infty} (x^2 + 1)^{-1}dx

​

For any R>0R > 0, expanding ff to the complex domain, and consider

$$\int_{C} \frac{1}{z^2 + 1}dz = 2\pi i Res(f, i) = 2\pi i \frac{1}{2 i} = \pi $$ Also we have

∫Cf(z)dz=∫CRlinef(z)dz+∫C(R,0,π)f(z)dz\int_{C} f(z)dz = \int_{C^{line}_R} f(z)dz + \int_{C(R,0,\pi)}f(z)dz

Therefore, we can write

lim⁡R→∞∫C1z2+1dz=lim⁡R→∞∫CRlinef(z)dz+lim⁡R→∞∫C(R,0,π)f(z)dz=π\lim_{R\rightarrow\infty} \int_{C} \frac{1}{z^2 + 1}dz = \lim_{R\rightarrow\infty} \int_{C^{line}_R} f(z)dz + \lim_{R\rightarrow\infty} \int_{C(R,0,\pi)}f(z)dz = \pi

Consider the latter term, because zf(z)=zz2+1→unif0zf(z) = \frac{z}{z^2+1}\rightarrow^{unif} 0 as z→∞z\rightarrow\infty, so that lim⁡R→∞∫C(R,0,π)f(z)dz=0\lim_{R\rightarrow\infty} \int_{C(R,0,\pi)}f(z)dz = 0 Note that

lim⁡R→∞∫CRlinef(z)dz=lim⁡R→∞∫−RRf(x)dx=∫−∞∞f(x)dx\lim_{R\rightarrow\infty} \int_{C^{line}_R} f(z)dz = \lim_{R\rightarrow\infty} \int_{-R}^R f(x)dx = \int_{-\infty}^\infty f(x)dx

so that

π=∫−∞∞1x2+1dx+0\pi = \int_{-\infty}^\infty \frac{1}{x^2 + 1}dx + 0

Jordon's Lemma

IF f(z)→unif0f(z)\rightarrow^{unif} 0 as z→∞z\rightarrow \infty and k>0k > 0 then

lim⁡R→∞∫C(R,0,π)eikzf(z)dz=lim⁡R→∞∫C(R,−π,0)eikzf(z)dz=0\lim_{R\rightarrow\infty} \int_{C(R, 0, \pi) } e^{ikz}f(z)dz = \lim_{R\rightarrow\infty} \int_{C(R, -\pi, 0) }e^{ikz}f(z)dz = 0

proof. parameterize C(R,0,π)C(R,0,\pi) with c(t):[0,π]→C,c(t)=Reitc(t):[0,\pi] \rightarrow \mathbb C, c(t)= Re^{it}

IR:=∣∫C(R,0,π)eikzf(z)dz∣=∣∫0πeikReitf(Reit)iReitdt∣=R∣∫0πekR(icos⁡t−sin⁡t)f(Reit)ieitdt∣≤R∫0π∣ekR(icos⁡t)∣e−kRsin⁡t∣∣ieit∣∣f(Reit)∣dt=R∫0πe−kRsin⁡t∣f(Reit)∣dt≤Rκ(R)∫0πe−kRsin⁡tdt=Rκ(R)2∫0π/2e−kRsin⁡tdt≤Rκ(R)2∫0π/2e−kR2tπdtsin⁡t≥2tπ.∀t∈[0,π/2]=2Rκ(R)π(1−e−πR)2Rk≤πkκ(R)\begin{align*} I_R&:=|\int_{C(R,0,\pi)} e^{ikz} f(z)dz|\\ &= |\int_0^\pi e^{ikRe^{it}} f(Re^{it}) iRe^{it}dt|\\ &= R|\int_0^\pi e^{kR(i\cos t- \sin t)} f(Re^{it}) ie^{it}dt|\\ &\leq R \int_0^\pi |e^{kR(i\cos t)}|e^{-kR\sin t}||ie^{it}| |f(Re^{it})| dt\\ &= R \int_0^\pi e^{-kR\sin t}|f(Re^{it})| dt\\ &\leq R \kappa(R) \int_0^\pi e^{-kR\sin t} dt\\ &= R \kappa(R) 2 \int_0^{\pi/2} e^{-kR\sin t} dt\\ &\leq R \kappa(R) 2 \int_0^{\pi/2} e^{-kR\frac{2t}{\pi}} dt &\sin t\geq \frac{2t}{\pi}. \forall t \in [0, \pi/2]\\ &= 2R\kappa(R) \frac{\pi (1-e^{-\pi R})}{2Rk}\\ &\leq \frac{\pi}{k} \kappa(R) \end{align*}

Since lim⁡R→∞κ(R)=0,lim⁡R→∞∣IR∣=0\lim_{R\rightarrow\infty} \kappa(R) = 0, \lim_{R\rightarrow\infty} |I_R| = 0

The proof for the second equation is similar

Example

∫−∞∞cos⁡xx2+1\int_{-\infty}^\infty \frac{\cos x}{x^2+1}

First, expand to complex domain,

cos⁡zz2+1=12eizx2+1+12e−izx2+1\frac{\cos z}{z^2+1} = \frac{1}{2}\frac{e^{iz}}{x^2+1} + \frac{1}{2}\frac{e^{-iz}}{x^2+1}

Let f1(z)=eizx2+1,f2(z)=e−izx2+1f_1(z) = \frac{e^{iz}}{x^2+1}, f_2(z) = \frac{e^{-iz}}{x^2+1}. We can compute f1f_1 on the top semicircle, and f2f_2 on the bottom semicircle.

lim⁡R→∞∮Cf1(z)dz=lim⁡R→∞∫CRlinef1(z)dz+lim⁡R→∞∫C(R,0,π)f1(z)dzRes(f1,i)=∫−∞∞eizx2+1dx+lim⁡R→∞∫C(R,0,π)eiz1x2+1dz2πilim⁡z→ieizz+i=∫−∞∞eizx2+1dx+0Jordon’s Lemmaπe=∫−∞∞eizx2+1dx\begin{align*} \lim_{R\rightarrow\infty}\oint_C f_1(z)dz &= \lim_{R\rightarrow\infty}\int_{C^{line}_R} f_1(z)dz + \lim_{R\rightarrow\infty}\int_{C(R, 0, \pi)} f_1(z)dz\\ Res(f_1, i) &= \int_{-\infty}^\infty \frac{e^{iz}}{x^2+1}dx + \lim_{R\rightarrow\infty}\int_{C(R, 0, \pi)} e^{iz}\frac{1}{x^2+1}dz\\ 2\pi i\lim_{z\rightarrow i} \frac{e^{iz}}{z+i} &= \int_{-\infty}^\infty \frac{e^{iz}}{x^2+1}dx + 0&\text{Jordon's Lemma}\\ \frac{\pi}{e} &= \int_{-\infty}^\infty \frac{e^{iz}}{x^2+1}dx \end{align*}

Simiarly,

lim⁡R→∞∮Cf2(z)dz=lim⁡R→∞∫−CRlinef2(z)dz+lim⁡R→∞∫C(R,−π,0)f2(z)dzRes(f2,−i)=−∫−∞∞e−izx2+1dx+lim⁡R→∞∫C(R,−π,0)e−iz1x2+1dz2πilim⁡z→−ie−izz−i=−∫−∞∞e−izx2+1dx+0Jordon’s Lemmaπe=∫−∞∞e−izx2+1dx\begin{align*} \lim_{R\rightarrow\infty}\oint_C f_2(z)dz &= \lim_{R\rightarrow\infty}\int_{-C^{line}_R} f_2(z)dz + \lim_{R\rightarrow\infty}\int_{C(R, -\pi, 0)} f_2(z)dz\\ Res(f_2, -i) &= -\int_{-\infty}^\infty \frac{e^{-iz}}{x^2+1}dx + \lim_{R\rightarrow\infty}\int_{C(R, -\pi, 0)} e^{-iz}\frac{1}{x^2+1}dz\\ 2\pi i\lim_{z\rightarrow -i} \frac{e^{-iz}}{z-i} &= -\int_{-\infty}^\infty \frac{e^{-iz}}{x^2+1}dx + 0&\text{Jordon's Lemma}\\ \frac{\pi}{e} &= \int_{-\infty}^\infty \frac{e^{-iz}}{x^2+1}dx \end{align*}

Therefore,

cos⁡zz2+1=12(2πe)=πe\frac{\cos z}{z^2+1} = \frac{1}{2}(2\frac{\pi}{e}) = \frac{\pi}{e}

Another convinient way is to notice

∫−∞∞eixx2+1dx=∫−∞∞cos⁡xx2+1dx+i∫−∞∞sin⁡xx2+1dx\int_{-\infty}^\infty \frac{e^{ix}}{x^2+1}dx =\int_{-\infty}^\infty \frac{\cos x}{x^2+1}dx + i\int_{-\infty}^\infty \frac{\sin x}{x^2+1}dx

Because sin⁡xx2+1\frac{\sin x}{x^2+1} is odd around 0, ∫−∞∞sin⁡xx2+1dx=0\int_{-\infty}^\infty \frac{\sin x}{x^2+1}dx = 0 and we are left with

πe=∫−∞∞eixx2+1dx=∫−∞∞cos⁡xx2+1dx\frac{\pi}{e} = \int_{-\infty}^\infty \frac{e^{ix}}{x^2+1}dx =\int_{-\infty}^\infty \frac{\cos x}{x^2+1}dx