Isoperimetric Inequality

Area of a Simple Closed Curve

Let \(\gamma: (0,L) \rightarrow \mathbb R^2, \gamma(s) = (x(s), y(s))\) be a simple closed unit-speed curve, \(\text{int}(\gamma)\) be the bounded interior. Then the area of \(\gamma\) is defined as

\[A(\gamma) = \iint_{\text{int}(\gamma)}dxdy \]

By Green's Theorem, we can instead integrating through the boundary, i.e.

\[\iint_S(\partial_x g - \partial f_y)dxdy = \int_{\partial S} (f(x, y)dx + g(x, y)dy)\]

Applied on the area integral, by taking \(f(x,y)= \frac{-y}{2}, g(x,y) = \frac{x}{2}\)

\[\begin{align*} A(\gamma) &= \iint_{\text{int}(\gamma)}dxdy \\ &= \int_{\gamma} (\frac{x}{2}dy - \frac{y}{2}dx)\\ &= \int_{\gamma} (\frac{x}{2}\frac{dy}{ds}ds - \frac{y}{2}dy\frac{dx}{ds}ds)\\ &= \frac{1}{2}\int_0^L x'(s)y(s) - x(s)y'(s) ds \end{align*}\]

Also, if we take \(f(x, y) = -y, g(x,y)=0\) or \(f(x,y) = 0, g(x,y)=x\), then

\[A = \int_0^L x(s)y'(s) ds = -\int_0^Lx'(s)y(s) ds\]

Geometric Interpratations

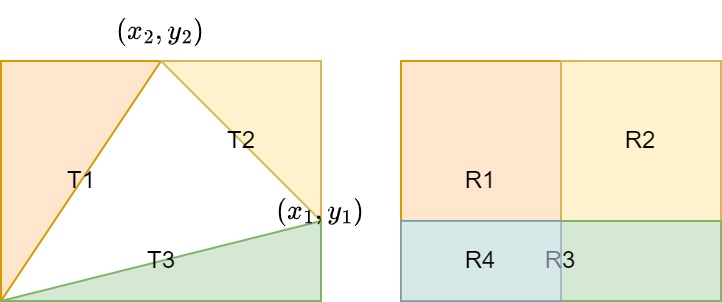
Lemma Consider a triangle \(A = (0, 0), B = (x_1,y_1), C = (x_2, y_2)\), WLOG assume \(x_1>x_2, y_1<y_2\). Then, its area is

\[A = \frac{1}{2}(x_1y_2 - x_2y_1)\]

proof.

\[\begin{align*} A &= R - T_1 - T_2 -T_3 \\ &= R - \frac{1}{2}(R_1+R_2+R_3)\\ &= R - \frac{1}{2}(Rec - R_4) \\ &= \frac{1}{2}R - R_4 \\ &= \frac{1}{2}(x_1y_2 - x_2y_1) \end{align*}\]

Claim For a polygon of \(n \geq 3\) points \(P_k = (x_k, y_k), k = 1,2,...,n\), its area is

\[A_n = \frac{1}{2}\sum_{i=1}^{n} x_i y_{i+1} - x_{i+1}y_i, P_{n+1} = P_0\]

proof. Let \(n = 3\), translating the polygon by \(-(x_1, y_1)\) and use the equation above.

Let \(n > 3\), then note that the polygon can be divided into a polygon \(P_1,...,P_{n-1}\) and a triangle \(P_{n-1}, P_{n}, P_1\). Therefore,

\[\begin{align*} A_n &= A_{n-1} + T_n\\ &= \frac{1}{2}(\sum_{i=1}^{n-2} (x_i y_{i+1} - x_{i+1}y_i) + x_{n-1}y_{1} - x_1y_{n-1}) \\ &\:+ \frac{1}{2}(x_{n-1}y_{n} - x_{n-1}y_{n} + x_ny_1 - x_1y_n + x_1y_{n-1} - x_{n-1}y_1)\\ &= \frac{1}{2}\sum_{i=1}^{n} (x_i y_{i+1} - x_{i+1}y_i) \end{align*}\]

Therefore, for a curve \(\gamma\), take each \(P_{k} = \gamma(s_k), P_{k+1} = \gamma(s_k + \Delta s) = (x_k + dx, y_k + dy)\),

\[\begin{align*} \tilde A &= \frac{1}{2}\sum_{i=1}^{n} (x_i (y_{i} + dy) - (x_i + dx)y_i)\\ &= \frac{1}{2}\sum_{i=1}^{n} x_idy - dxy_i\\ A &= \frac{1}{2}\int_\gamma xdy-ydx \end{align*}\]

Isoperimetric Inequality (E. Schmidt)

Claim For a simple closed curve \(\gamma(s) = (x(s), y(s))\) with length \(L\) and area \(A\). Then \(A\leq \frac{L^2}{4\pi}\). Moreover, \(A = \frac{L^2}{4\pi}\) IFF \(\gamma\) is a circle.

proof. Since \(\gamma\) is a simple closed curve, Take \(x_0 = \min(x(s)), x_1 = \max(x(s)), w= x_1-x_0\), take \(R = \frac{w}{2}\).
Let \(C\) be a circle of radius \(R\) centered at \((0, 0)\). WLOG, translate \(\gamma\) by \((-\frac{x_0+x_1}{2}, 0)\) so that \(x_0=-R, x_1=R\).
Parameterized \(C\) by projecting \(\gamma\) to the circle. i.e. \(c(s) = \text{proj}(x(s), y(s)) = (x(s), \hat y(s))\) where \(x(s)^2 + \hat y(s)^2 = R^2\). Note that \(c\) is not regular.

For each \(s\), look at its projection to the outer unit normal \(-\mathbf n_s(s) = (y'(s), -x'(s))\) (rotating tangent clockwise by \(\pi/2\)). Take \(\text{proj}_c\) to be the projection from \(c(s)\) to \(-\mathbf n_s(s)\),

\[\begin{align*} &\text{proj}_c(s) (x(s), \hat y(s)) \cdot (y'(s), -x'(s))\\= &\|c(s)\| \|-\mathbf n_s(s)\|\cos(\alpha(s))\\= &R\cos(\alpha(s)) \leq R \end{align*}\]

where \(a\) is the angle between \((x,\hat y), (y',-x')\) Note that \(\text{proj}_c(s) = R\iff \alpha(s) = 0\) IFF the outer normal is directed exactly the same as the vector on the circle.
Also, we have the inequality

\[xy'-x'\hat y = (x, \hat y) \cdot (y', -x') \leq R\]

and integrating along the curve

\[\begin{align*} \int_0^L (xy'-x'\hat y) ds &\leq RL\\ \int_0^L xy' ds+ (- \int_0^L x'\hat y ds) &\leq RL\\ A + \pi R^2 &\leq RL &\text{Green's Theorem}\\ A &\leq LR - \pi R^2 = \frac{L^2}{4\pi} - \frac{\pi}{4}(\frac{L}{\pi} - 2R)^2\\ A &\leq \frac{L^2}{4\pi} \end{align*}\]

Then, consider the conditions for the equality. First, we must have \(L = 2\pi R\) from the computations above, and this must be try for each direction. Also, we must have that for all \(s, \alpha = 0 \iff (x,\hat y) \perp (x',y')\).

Isoperimetric Inequality (Steiner)

Fact 1 \(A\leq \pi L^2\), i.e. the curve can be contained within a circle of radius \(L\)

Fact 2 \(\gamma\) is convex.
Suppose that the line segment \(\gamma(s_0), \gamma(s_1)\) is not contained in \(\text{int}(\gamma)\), then flip \(\gamma([s_0, s_1])\) around the line segment and we can get a larger area with the same arc length.

Fact 3 If \(\gamma\) is convex, then \(\kappa_s(s)\) does not change its sign for all \(s\).

Fact 4 For any point \(P\) on a circle \(C\), and a diameter \(AB\), for the triangle formed by \(P, A, B\), the angle at \(P, \theta_P = \pi/2\).

Claim If for any simple closed plane curve of length \(L\), exists some curve \(\gamma\) that attains the maximum, then \(\gamma\) is a circle of \(R = \frac{L}{2\pi}\).

Note that the assumption (existence of maximum won't not proved here)

proof. Take some convex \(\gamma\) be the curve that attains maximum area, take \(a,b\) s.t. each \(\gamma([a, b)) = \gamma([b, a)) = L/2\). Then, \(\text{int}(\gamma)\) is divided into two parts, call then \(D_1, D_2\) with area \(A_1, A_2\). Then, we must have that \(A_1 = A_2\), otherwise we can find a curve with larger area by flipping the larger half. Therefore, we have that for all \(P_1, P_2\) that divides the arc into 2 equal pieces, the divided areas must be equal.

Then, we want to show that \(D_1\) and \(D_2\) are both semicircles with diameter \(P_1P_2\), by Fact 4, equivalently we want to show that \(\theta_p = \pi/2\) for any \(P\) on the curve.

Suppose \(D_1\) is not a semicircle, then take some \(P\) s.t. \(\theta_P\neq \pi/2\).

Then, consider the domain enclosed by the line segment and curve between \(PP_1\) and the line segment and curve between \(PP_2\). We can rotate the two domains around \(P\) so that \(\theta_P = \pi/2\). Note that the area of the triangle formed by \(PP_1P_2\) has its maximum when \(\theta_P=\pi/2\), the area of other 2 domains does not change, the arc length does not change. Therefore, by contradiction, we proved that \(\theta_P = \pi/2\) for all \(P\).

Example: Isoperimetric Inequality on Ellipse

Claim. Let the ellipse be defined as \(\frac{x^2}{p^2} + \frac{y^2}{q^2} =1\). Then, we have that

\[\int_0^{2\pi} \sqrt{p^2\sin^2 t + q^2\cos^2t} dt \geq 2\pi \sqrt{pq}\]

with equality IFF \(p=q\).

proof. Let \(\gamma(t) = (p\cos t, q\sin t)\) be the parameterization of the ellipse. so that \(\gamma'(t) = (-p\sin t, q\cos t)\). and the arc-length

\[L = \int_0^{2\pi} \|\gamma'(t)\| dt = \int_0^{2\pi} \sqrt{p^2\sin^2 t + q^2\cos^2t} dt\]

and the area of the ellipse is

\[A = \frac{1}{2}\int_0^{2\pi} p\cos t q\cos t + p\sin t q\sin t = \frac{1}{2}pq\int_0^{2\pi} dt = \pi pq\]

By Isoperimetric Inequality,

\[\begin{align*} L &\geq \sqrt{4\pi A}\\ \int_0^{2\pi} \sqrt{p^2\sin^2 t + q^2\cos^2t} dt &\geq \sqrt{4\pi^2 pq}\\ \int_0^{2\pi} \sqrt{p^2\sin^2 t + q^2\cos^2t} dt &\geq 2\pi\sqrt{pq} \end{align*}\]

\(p=q\) IFF the ellipse is a circle IFF Isoperimetric equality holds.