Cauchy's Theorem

Theorem Let \(f:D\rightarrow \mathbb C\) be analytic on simply connected domain \(D\). For any Jordon contour \(C\subset D\), \(\oint_C f(z)dz = 0\)

proof (simpler ver.). We will prove the statement with the assumption that \(f'\) continuous on \(D\),

Remark that Greens theorem states that for real functions \(f:\mathbb R^2 \rightarrow\mathbb R^2, f(x, y) = \begin{pmatrix}u(x,y\\v(x,y)\end{pmatrix}\) and a simple closed contour \(C\),
If the partial derivatives \(u_x, u_y, v_x, v_y\) are continuous on the region \(R = C\cup C_{int}\), then

\[\oint_C (udx + vdy) = \iint_{R}(v_x - u_y)dxdy\]

Then, consider its connection to \(f = u+iv\) on the same region.

\[\begin{align*} \oint_C f(z)dz &= \oint_C u(x,y) + i(x,y) (dx+idy)\\ &=\oint_C udx -vdy + i\oint_C udy + vdx\\ &= \iint_R (-v_x - u_y)dxdy + \iint_R (u_x-v_y)dxdy &\text{Green} \\ &= \iint_R (u_y - u_y) dxdy + \iint_R (u_x-u_x)dxdy&\text{CR}\\ &= 0 \end{align*}\]

Deformation of Curves

Note that for any two endpoints \(z_0, z_1 \in D\), \(D\) is simply connected. Then, arbitrarily pick two curves \(C_1, C_2\) traverse from \(z_0\) to \(z_1\), then \(C_1, \neg C_2\) will form a simple closed curve, so that \(\oint_{C_1\cup\neg C_2} = 0\implies \oint_{C_1} = \oint_{C_2}\)

Example Define a branch of \(\log\) as \(D = \{re^{i\theta} : r > 0, \theta \in (-\pi, \pi)\}\). Therefore, we can define its anti-derivative as \(z^{-1}\) on this branch by

\[L(z_1) = \int_1^{z_1}z^{-1}dz = \log(r) + i\theta - \int_1^1 z^{-1} = \log(r) + i\theta \]

Theorem 1

For \(f:D\rightarrow \mathbb C\) continuous. If \(\forall C\subset D\) be simple closed contours \(\oint_C f(z)dz = 0\), then \(\exists F:D\rightarrow\mathbb C\) s.t. \(F\) is analytic and \(F' = f\).

proof. We will assume \(D\) is convex, otherwise, we need to construct path with multiple line segments within a union of convex regions and it will be unnecessarily messy.

Fix some point \(z_0\in D\), define \(F(z_1) := \int_{z_0}^{z_1} f(z)dz\). Note that we can define the integral on any curve from \(z_0\) to \(z_1\), but here we'll specifically choose the line segment with the assumption that \(D\) is convex, so that the path is always within \(D\).

Fix arbitrarily small \(h\), Note that \(z_0\rightarrow z_1+h\rightarrow z_1\rightarrow z_0\) encloses a region within \(D\) so that

\[F(z_1+h) - F(z_1) = \int_{z_0}^{z_1+h}f(z)dz - \int_{z_0}^{z_1}f(z)dz = \int_{z_1}^{z_1+h}f(z)dz\]

Therefore, we can write

\[\begin{align*} \lim_{h\rightarrow 0}\frac{F(z_1+h) - F(z_1)}h &= \lim_{h\rightarrow 0} \big(h^{-1}\int_{z_1}^{z_1+h}f(z)dz - h^{-1}\int_{z_1}^{z_1+h}f(z_1)dz + f(z_1)\big)\\ &= \lim_{h\rightarrow 0} \big(h^{-1}\int_{z_1}^{z_1+h}(f(z) - f(z_1))dz\big) + f(z_1) \end{align*}\]

Then, since \(f\) is continuous on \(D\), for arbitrarily small \(\epsilon > 0\), we can take \(\delta > 0\) so that for any \(z \in B_\delta(z_1)\), \(|f(z)-f(z_1)|\leq \epsilon\). Therefore, by ML inequality

\[h^{-1}\int_{z_1}^{z_1+h}(f(z)-f(z_1))dz \leq h^{-1}h\epsilon = \epsilon\]

By the definition of limit

\[\lim_{h\rightarrow 0} h^{-1}\int_{z_1}^{z_1+h}(f(z)-f(z_1))dz = 0\]

So that we have

\[F'(z_1) = \lim_{h\rightarrow 0}\frac{F(z_1+h) - F(z_1)}h = 0 + f(z_1) = f(z_1)\]

Corollary (An easier statement of CT)

For \(f:D\rightarrow\mathbb C\) continuous and \(F:D\rightarrow \mathbb C\) analytic. If \(\forall z\in D. F'(z) = f(z)\) and \(C\subset D\) is a Jordan Contour. Then \(\oint_C f(z)dz = 0\)

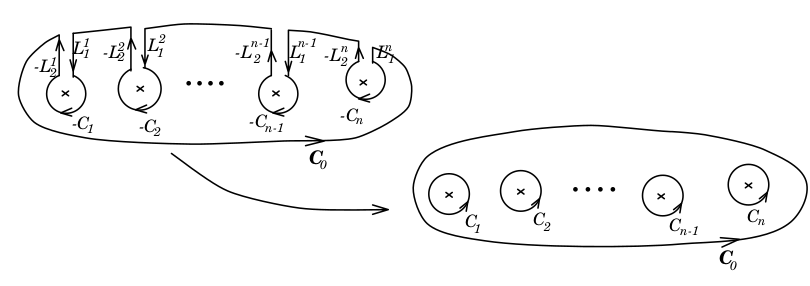
Deformation of Contours

Consider \(f:D\rightarrow \mathbb C\) is analytic everywhere except for a points \(z_0, z_1, ...\) and \(D\) is simply connected. For a Jordan Contour \(C\) such that points \(z_0, z_1,... \in C_{int}\). We can construct Jordan curves \(C_0, C_1,...\) that encloses \(z_0, z_1,...\), respectively so that

\[\oint_C f(z)dz = \sum_{i=0}\oint_{C_i}f(z)dz\]

proof. For each \(C_i\), take line segments \(L_i^1, L_i^2\) connecting \(C_i, C\) and start and end points of \(L_i^1, L_i^2\) be arbitrarily close. Then, we construct path

\[\tilde C = C +\sum_{i=0}-C_i + L_i^1 - L_i^2 = C -\sum_{i=0}C_i\]

Note that \(\tilde C\) does not enclose any of \(z_o, z_1,...\) so that by Cauchy's Theorem, \(\oint_{\tilde C} = 0\), so that \(\oint_C = \sum \oint_{C_i}\)