Registration

Problem

When we scan a rigid object, we should have multiple scans from different positions and angles. However, if we don't match/align these scans, they are just multiple partial scans. Therefore, we need some way to register these points, i.e. find a spatial transformation that maps one scan to the alignment of the other.
Another possible case is that we can have a coarse scan of a person and a finer scan of the face. We need to register the face.

We start with a complete scan of the surface \(Y\) and a new partial scan of the surface \(X\), both of them are which triangle meshes, they may not have the same number of vertices or even the same topology.

Hausdorff Distance

To measure the performance of the matching, we need a single scalar number, i.e. distance.

Point-Point Distance

We can start with point to point Euclidean distance, for points \(x, y\), let

\[d(x,y) = \|x-y\|_2\]

Point-Projection Distance

Then, consider the distance between a point \(x\) and some large object \(Y\), let

\[d(x,Y) = \inf_{y\in Y} d(x, y)\]

Directed Hausdorff Distance

Let the directed Hausdorff distance be

\[D_{\vec H}(X, Y) = \sup_{x\in X}\|x-P_Y(x)\|\]

where \(P_Y(x)\) is the closest-point projection from \(x\) to \(Y\).
Note that we use supremum, which means the worst projection is at most this distance.
Also, note that this distance is "directed", i.e. \(D_{\vec H}(X,Y) \neq D_{\vec H}(Y, X)\).

DHD Between Triangle Meshes

Since we have the two triangle Meshes, we can approximate a lower bound on the Hausdorff distance by densely sampling surfaces \(X\) as \(\mathcal P_X\). Obviously,

\[D_{\vec H}(X, Y) \geq D_{\vec H}(\mathcal P_x, Y)\]

And as we have more samples, it's more likely to approach the true distance.

However, note that the \(\max\) function is not continuous, hence hard to optimize.

Random Sampling of a Mesh

We want our random variable \(x\in X\) to have a uniform density \(f=A_X^{-1}\), where \(A_X\) is the surface area of \(X\). Therefore, we break the steps into randomly sample individual triangle, and then sample point from that triangle.
Let \(h(T) = \frac{A_T}{A_x}\) be the uniform distribution over triangle index \(T\in\{1,...,m\}\), \(g_T(x) = A_T^{-1}\) be the uniform distribution over the triangle \(T\), then

\[h(T)g_T(x) = \frac{A_T}{A_X}\frac1{A_T} = A_X^{-1} = f(x)\]

Uniform random sampling of a single triangle.

Let \(v_1,v_2, v_3\) be the corners of the triangle, first pick a point uniformly in the parallelogram form by reflecting \(v_1\) across the line \(\overline{v_2v_3}\). Then, randomly sample \(a_1, a_2 \in [0, 1]\)

\[x = \begin{cases}v_1 + a_1(v_2-v_1) + a_2(v_3-v_1)&a_1+a_2 \leq 1\\v_1 + (1-a_1)(v_2-v_1) + (1-a_2)(v_3-v_1)&a_1+a_2 < 1\end{cases}\]

In case 2, we sampled a point in the reflection part of the triangle, hence we reflect it back by \(1-a\)

Area-weighted Random Sampling of Triangles

Let \(\mathcal C_i = \sum^i_{j=1}\frac{A_j}{A_X}\) be the cumsum of the relative areas. Then we randomly sample \(a\in [0, 1]\) and locate the index of \(a\) in that cumsum interval.

Integrated Closest-Point Distance

To enable optimization, we replace the sup norm with the euclidean norm, i.e.

\[D_{\vec C}(X, Y) = \sqrt{\int_{X}\|x-P_Y(x)\|^2 dA}\]

So that we can define the directed matching energy from \(Z\) to \(Y\) as

\[E_{\vec C}(Z, Y) = [D_{\vec{C}}(Z,Y)]^2 = \int_{Z}\|z-P_Y(z)\|^2 dA = \int_Z \|f_Y(z)\|^2 dA\]

Consider the function \(f_Y(z) = z - P_Y(z)\). if \(P_Y(z)\) is a point, that \(f(z) = z-y\) is linear, and if \(Y = \{y\mid (y-p)\cdot n = 0\}\) is a infinite plane, then \(f_Y(z) = ((z-p)\cdot n)n\) is also linear. However, due to "smallest" distance, the linearity does not hold and \(f_Y\) may not even be continuous.

However, if we fix some \(z_0\) s.t. \(f(z) = z-P_Y(z_0)\), since \(z_0\) is fixed, and \(P_Y(z_0)\) is a point. the function can be optimized, takes one step further, we can do \(f_Y(z) = ((z-P_Y(z_0))\cdot n)n\), which also can be optimized. Therefore, we can have an iterative algorithm

z_0 = initial guess
while not converge:
    f = linearize f(z) around z_0
    z_0 = minimize f(z)^2

ICP: Iterative Closest Point Algorithm

Go back to the original problem, our task is to find a rigid transformation \(T\)

\[T(x) = Rx + t\]

where \(R\in SO(3)\) is the rotation matrix and \(t\in\mathbb R^3\) is the translation vector, and our problem is to

\[\arg\min_{t, R}\int_X \|Rx + t - P_Y(Rx + t)\|^2 dA\]

which, as we sampled points on \(X\), is approximated as

\[\arg\min_{t, R} \sum_{\mathcal P_x} \|Rx + t - P_Y(Rx + t)\|^2 \]

Procedure

The procedure can be described as below

ICP(V_X F_X, V_Y, F_Y)

# init R, t, possibly as identity and zero vector
R = identity(3)
t = [0, 0, 0]
while not converge:
    X_points = sample from V_X F_X
    proj = project all X_points onto V_Y F_Y
    R, t = update rigid transformation from best matched X_points and proj
    V_X = R(V_X) + t

Then, we have to consider the methods fro the rigid transformation update. As from previous discussions, we can do point-to-point or point-to-plane.

Point-Point Rigid Matching

We are trying to solve

\[\arg\min_{R, t} \sum^k \|Rx_i + t - p_i\|^2\]

The energy is quadratic in \(t\), so that the optimal \(t^*\) can be obtained by (with unknown \(R\))

\[\begin{align*} \partial_t\|RX^T + t\vec 1^T - P^T\|_F^2 &= 0\\ \vec 1^T1t + RX^T\vec 1 - P^T\vec 1 &= 0\\ t&=\frac{P^T\vec 1 -RX^T\vec 1}{\vec 1^T\vec 1}\\ t &= \bar p - R\bar x \end{align*}\]

where \(X_{k\times 3}, P_{k\times 3}\) are \(x_i, p_i\) stacked vertically, and \(\vec 1_{k\times 1}\) is the vector filled with 1's. \(\|\cdot\|_F\) is the Frebenius norm, which is the sum of squared elements. \(\bar p = k^{-1}\sum^k p_i, \bar x = k^{-1}\sum^k x_i\) is the mean of all points.

Then, replace \(t = \bar p - R\bar x\), the problem becomes

\[\begin{align*} R^* &= \arg\min_{R} \sum^k \|Rx_i + (\bar p - R\bar x) - p_i\|^2\\ &= \arg\min_{R} \sum^k \|R(x_i-\bar x) - (p_i - \bar p)\|^2\\ &= \arg\min_{R} \| R\bar X^T - \bar P^T\|^2_F \end{align*}\]

where \(\bar X_{k\times 3}, \bar P_{k\times 3}\) are \(x_i-\bar x, p_i - \bar p\) stacked vertically.

Then,

\[\begin{align*} R^* &= \arg\min_{R} \| R\bar X^T - \bar P^T\|^2_F\\ &= \arg\min_{R} \|R\bar X^T\|_F^2 - 2\langle R\bar X^T, \bar P^T\rangle_F + \|\bar P^T\|^2_F\\ &= \arg\min_{R} \|\bar X^T\|_F^2 - 2\langle R\bar X^T, \bar P^T\rangle_F + \|\bar P^T\|^2_F &R\in SO(3)\Rightarrow R^TR = I\\ &= \arg\max_{R} \langle R\bar X^T, \bar P^T\rangle_F\\ &= \arg\max_{R} \langle R, \bar P^T\bar X\rangle_F &\text{permutation property of F-norm} \end{align*}\]

Closest Rotation Matrix

Using SVD, we can have \(\bar P^T\bar X = U\Sigma V^T\), so that with permutation property of F-norm again

\[R^* = \arg\max_R\langle R, U\Sigma V^T\rangle = \arg\max_R\langle U^TRV, \Sigma\rangle\]

Let \(\Omega = U^TRV\) with \(\det \Omega = \det UV^T\), since \(U,V\) are orthonormal, \(\Omega^T = \Omega^{-1}\). This implies that \(R^* = U\Omega^*V^T\), where

\[\Omega^* = \underset{ {\Omega\in O(3), \det\Omega = \det UV^T} }{\arg\max} \langle \Omega, \Sigma\rangle_F\]

so that \(\det R^* = 1\).

Because \(\Omega\) is orthonormal, each col and row must have unit norm. Placing a non-zero on the off-diagonal will get "killed" when multiplied by the corresponding zero in \(\Sigma\). So the optimal choice is to set all values 0, except the diagonal. The best choice is

\[\Omega^* = \begin{bmatrix}1&0&0\\0&1&0\\0&0&\det UV^T\end{bmatrix}\]

so that \(\det UV^T\) is multiplied with the smallest \(\sigma\). finally the closest rotation matrix is obtained as

\[R^* = U\Omega^*V^T\]

Point to Plane Rigid Matching

We are trying to solve

\[\arg\min_{R, t} \sum^k \|(Rx_i + t - p_i)\cdot \hat n_i \hat n_i\|^2\]

where \(\hat n_i\) is the unit normal at the located closest point \(p_i\). The problem can be simplified a bit as

\[\arg\min_{R, t} \sum^k ((Rx_i + t - p_i)\cdot \hat n_i)^2\]

To optimize \(R\), we linearize the constraint that \(R\) stays a rotation matrix and work with a reduced set of variables. Any rotation matrix can be written as scalar rotation angle \(\theta\) around a rotation axis defined by a unit vector \(\hat w\), generally, given the rotation axis, the axis-angle to matrix formula gives

\[R_{\hat w}(\theta) = I + \sin\theta W + (1-\cos\theta)W^2\]

where \(W\) is the skew symmetric cross product matrix

\[Wx = \hat w\times x, W = \begin{bmatrix}0&-w_3&w_2\\w_3&0&-w_1\\-w_2&w_1&0\end{bmatrix}\]

In this form, we can linearize by considering a small change in \(\theta\) and \(\hat w\), as

\[R\approx I + \theta W, Rx \approx x + \theta \hat w \times x\]

introducing \(a = \theta \hat w\), the problem becomes

\[\arg\min_{a,t} \sum^k ((x_i + a\times x_i + t - p_i)\cdot \hat n_i)^2\]

and let \(u = \begin{bmatrix}a\\t\end{bmatrix}\),

\[\arg\min_u \sum^k \big(\begin{bmatrix}(x_i\times \hat n_i)^T &\hat n_i^T\end{bmatrix}u - \hat n_i^T (p_i - x_i)\big)^2\]

Then, let \(c_i = \begin{bmatrix}(x_i\times \hat n_i)^T &\hat n_i^T\end{bmatrix}, d_i = \hat n_i^T (p_i - x_i)\), the equation above is expanded as

\[\arg\min_u \sum^k u^Tc_i^Tc_iu-2u^Tc_i^Td_i + d_i^Td_i = \arg\min_u \sum^k u^TAu-2u^Tb\]

where \(A = \sum^k c_i^Tc_i, b = \sum^kc_i^Td_i\)

Therefore, \([a^*, t^*] = u^* = A^{-1}b\), as we considering \(A\) as a sum of \(c_i\), which is convex and separable. Then, we have \(a^* = \underset{\theta}{\|a^*\|}\underset{\hat w}{\frac{a^*}{\|a^*\|}}\), and we can find

\[R^* = I + \sin\theta W^* + (1-\cos\theta) [W^*]^2\]

Some Additional Pieces

Uniform random sampling of a triangle mesh

To uniform sampling a mesh \(X\), the pdf will be

\[f_X(x) = A_X^{-1}\]

we can then have two independent uniform random sampling, first, sample a triangle from \(T=\{1,2,...,m\}\) of the mesh, which \(h_i = \frac{A_i}{A_X}\) and then for each triangle, sample from \(g_i(x) = A^{-1}_i\), so that

\[f_X(x) = h(T)g_T(x) = \frac{A_T}{A_X}\frac{1}{A_T} = A_X^{-1}\]

Consider \(g_T\), a triangle can be written as parametric function \(T(s, t) = a + s(b-a) + t(c-a)\) where \(0<s, t<1, s+t\leq1\). Also, note that if we release the constraint \(s+t\leq1\), we get a parallelgram formed by reflecting \(a\) across \(\bar{bc}\). Therefore, we can randomly sample \(s, t\) and if \(s+t > 1\), we reflect it back by \(1-s, 1-t\)

Area Weighted random Sampling of Triangles

Note that the cmf of \(h\) is

\[C(i) = \sum_{j=1}^i \frac{A_j}{A_X} \in (0, 1]\]

Therefore, we can randomly sample \(x\) and find the first value of \(C_i\) s.t. \(C_i > x\)

Point Triangle Distance

Given a query point \(x\in\mathbb R\) and triangle \(T\in \mathbb R^{3\times 3}\) with corners \(a, b,c\). To find \(p\) s.t.

\[p=\arg\min_{p\in T}\|x-p\|\]

Let \(P\) be the plane that \(T\) belongs to, we can simply define \(P\) from \(T\), but remove the constraints.

\[P(s,t):\mathbb R^2\rightarrow\mathbb R^3:= a + s(b-a) + t(c-a)\]

Let \(q \in P\) be the point projected from \(x\) to \(P\). Then,

\[\|x-p\| = \|(x-p) + (p-q)\|\]

Note that \(x, q\) is fixed, so that we want to minimize \(\|p-q\|\), note that \(p,q\) both line on \(P\), thus this problem becomes a 2D problem on the plane \(P\).

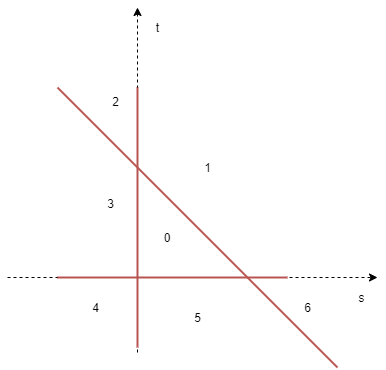
Then, to solve the 2D problem. Note that the regions are divided by \(s=0, t=0, s+t=1\), we can do it case by case. - 0 => within the triangle, done - 1, 3, 5 -> point-line projection, if not on the segment range, then map it to the endpoint - 2, 4, 6 -> directly go to the endpoint

An efficient implementation will try to reduce the number of divisions, so that the relative error is small (See Reference here)