Shader Pipeline
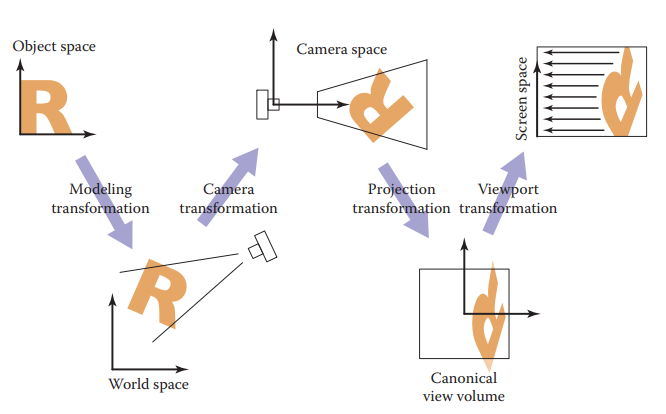
Viewing Transformations
The viewing transformations inputs a canonical coordinate \((x, y, z)\) to some \((x, y)\) on the 2D image space. One common system is a sequence of 3 transformations - camera transformation \((x, y, z)\rightarrow (x_c, y_c, z_c)\) given \(eye\) and orientation \(u, v, w\) - projection transformation \((x_c, y_c, z_c) \rightarrow (x_v, y_v)\), \(x_v, y_v\in [-1, 1]\) all the points that are visible in the camera space given the type of projection desired - viewport transformation \((x_v, y_v)\rightarrow (I_x, I_y)\) maps the unit image rectangle to desired rectangle in pixel coordinates
Perspective Projections
Shader Pipeline (OpenGL)
Vertex specification
Set up Vertex Array Object (VAO), which contains one or more Vertex BUffer Objects (VBO), each VBO stores some information about each vertex. For example, if we load a .obj file, then VAO (the object) may end up having several VBOs, for example, one VBO stores vertex positions, one VBO stores vertex colors, and another one stores vertex normals.
Vertex shader
Performs operation on every vertex, doing all the homogeneous transformations, i.e.
- \(M\): modeling transformation: to move object into world space, doing all the translations, rotations, scaling, etc.
- \(V\) viewing transformation/camera transformation: transforms from world coordinates to camera coordinates.
- \(P\) perspective projection matrix, so that we only consider vertex in the window space (visible within the camera), and normalize \((x, y, z)\) by \(w\).
Tessellation
patches of vertex data are subdivided into smaller Primitives. Tessellation control shader (TCS) determines how much tessellation to do and tessellation evaluation shader (TES) takes the tessellated patch and computes vertex values for each generated vertex.
For example Catmull–Clark subdivision can be a TCS/TES algorithm.
Rasterization
Given the tessellated primitives, filled in the primitive with pixels.
Fragment shader
Given a sample-sized segment of a rasterized Primitive, fragment shader computes a set of colors and a single depth value. In our cases, it will be pixel-wise coloring.
Note that the shader pipeline is only for OpenGL. In other frameworks (WebGL, DirectX, etc.) the abstractions are different. For example, WebGL does not have support for tessellation and you have to do it in js (likely on CPU).
varying vec3 vViewPos;
void main() {
vPos = position;
vViewPos = (modelViewMatrix * vec4(position, 1.0)).xyz;
vNormal = normalMatrix * normalize(normal);
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);;
}
`
// fragment shader using Blinn Phong shading
vec3 blinn_phong(vec3 ka, vec3 kd, vec3 ks, float p, vec3 n, vec3 v, vec3 l) {
float Ia = 0.4;
vec3 h = normalize(v+l);
return ka*Ia + kd*max(dot(l,n),0.0) + ks*pow(max(dot(h,n),0.0),p);
varying vec3 vPos;
varying vec3 vNormal;
varying vec3 vViewPos;
void main() {
vec3 l = mat3(viewMatrix) * normalize(vec3(1, -1, -1));
vec3 n = normalize(vNormal);
vec3 v = normalize(-vViewPos);
vec3 color = mix(vec3(0.9,0.2,0.3), vec3(0.5,0.45,0.5), is_moon);
vec3 fragColor = blinn_phong(
color, color, vec3(1.0, 1.0, 1.0), 300.0,
n, v, l
);
gl_FragColor = vec4(fragColor, 1.0);
}
Value Noise and Procedural Patterns
Other than a texture mapping, we can also generate patterns, i.e. procedural patterns. For example, if we want to make a ocean texture, we can generate some waves mesh and color it by some algorithm, instead of map a 2D image onto it.
Noise
Note that in reality, lots of patterns need some sort of "randomness", s.t. the volume of a cloud on the sky, the waves of the water, etc.
Properties of Ideal Noise
- pseudo random Given the same input, it should always return the same value.
- dimension The noise function is some \(N:\mathbb R^d\rightarrow \mathbb R\), which is a \(d\)-dim noise function.
- band limited One of the frequencies dominates all others.
- continuity / differentiability We want the change in local is small, but change in global is large
Perlin Noise
Perlin noise is a example of value noise, it's pseudo random, and continuous, and good in producing marble like surfaces.
Algorithm
Grid Definition
Define an n-dim grid where each point has a random n-dim unit-length gradient vector.
Dot product
Assume \(3D\) case and each box grid has side length 1. For query position \((x, y, z)\), it is located in some \(d\)-dim grid formed by \(2^3\) grid points, \((\lfloor x\rfloor, \lceil x\rceil)\times (\lfloor y\rfloor, \lceil y\rceil)\times (\lfloor z\rfloor, \lceil z\rceil)\). Generate \(2^d\) dotGridGradient by dot product the offset to each grid point and gradient at that grid point.
Interpolation
Note that we have \(2^3\) scale values, and we will have a trilinear interpolation so that we can get the value at that point.
Note that we take a smooth step \(s:\mathbb R^d\rightarrow \mathbb R^d\) as the coefficient of interpolation. \(s\) must have the property \(s(0) = s(1) = s'(0) = s'(1) = 0\), one good smooth step function is
Improved Perlin Noise
Note that \(s''(t) = 6 - 12t\) is not continuous, if the derivative of the function used to compute the normal of the displaced mesh is not continuous then it will introduce a discontinuity in these normals wherever \(x=0, 1\), so that we use improved smooth step
Also, note that when random directions (gradient direction) is close to standard direction \(e_i\), the noise function have very high values \(\sim1\) causing a "splotchy appearance", so instead of using random directions, we use directions randomly chosen from 12 directions \((\pm 1,\pm 1,0), (\pm 1, 0, \pm 1), (0, \pm 1, \pm 1)\)
vec3 random_direction(vec3 seed) {
vec2 r2 = random2(seed);
float z = 2.0 * r2.x - 1.0;
float a = r2.y * 2.0 * 3.1415926;
float r = sqrt(1.0 - z*z);
return vec3(z, r * cos(a), r * sin(a));
}
vec3 smooth_step(vec3 f) {
return f * f * (3.0 - 2.0 * f);
}
// The improved version
vec3 smooth_step( vec3 f) {
return 6.0*f*f*f*f*f - 15.0*f*f*f*f + 10.0*f*f*f;
}
float perlin_noise(vec3 st) {
vec3 i = floor(st);
vec3 f = fract(st);
vec3 u = smooth_step(f);
float dotgrad000 = dot(random_direction(i + vec3(0.0, 0.0, 0.0)), f - vec3(0.0, 0.0, 0.0));
float dotgrad001 = dot(random_direction(i + vec3(0.0, 0.0, 1.0)), f - vec3(0.0, 0.0, 1.0));
float dotgrad010 = dot(random_direction(i + vec3(0.0, 1.0, 0.0)), f - vec3(0.0, 1.0, 0.0));
float dotgrad011 = dot(random_direction(i + vec3(0.0, 1.0, 1.0)), f - vec3(0.0, 1.0, 1.0));
float dotgrad100 = dot(random_direction(i + vec3(1.0, 0.0, 0.0)), f - vec3(1.0, 0.0, 0.0));
float dotgrad101 = dot(random_direction(i + vec3(1.0, 0.0, 1.0)), f - vec3(1.0, 0.0, 1.0));
float dotgrad110 = dot(random_direction(i + vec3(1.0, 1.0, 0.0)), f - vec3(1.0, 1.0, 0.0));
float dotgrad111 = dot(random_direction(i + vec3(1.0, 1.0, 1.0)), f - vec3(1.0, 1.0, 1.0));
float x00 = mix(dotgrad000, dotgrad100, u.x);
float x01 = mix(dotgrad001, dotgrad101, u.x);
float x10 = mix(dotgrad010, dotgrad110, u.x);
float x11 = mix(dotgrad011, dotgrad111, u.x);
float xy0 = mix(x00, x10, u.y);
float xy1 = mix(x01, x11, u.y);
return mix(xy0, xy1, u.z);
}
Bump Mapping and Normal Mapping
The real surface is often rough and bumpy, we use bump mapping algorithm to achieve the same effect.
where \(p\) is the original position, \(\hat n\) is the normal and \(h\) is the bump height function.
Then, note that we have to calculate a new normal for the bumped point as
where \(T, B\) are the tangent and bitangent vector where
Note that bump mapping does not actually change the vertex position, it is used to obtain the normal mapping so that we can apply the coloring and make the surface looks "bumpy"
vec3 bp = bump_position(is_moon, sphere_fs_in);
float eps = 0.0001;
vec3 T;
vec3 B;
tangent(n,T,B);
vec3 pT = sphere_fs_in+eps*T;
vec3 pB = sphere_fs_in+eps*B;
n = normalize(cross(
bump_position(is_moon, pT)-bp,
bump_position(is_moon, pB)-bp));
n = normalMatrix * normalize(n);
Shader Demo
A demo of shaders, noise, and bump mapping
Shader code
// Shader programs are merely strings and are only
// loaded onto GPU
const blinn_phong = `
vec3 blinn_phong(vec3 ka, vec3 kd, vec3 ks, float p, vec3 n, vec3 v, vec3 l) {
float Ia = 0.4;
vec3 h = normalize(v+l);
return ka*Ia + kd*max(dot(l,n),0.0) + ks*pow(max(dot(h,n),0.0),p);
}
`
const random_direction = `
// pseudo-random 2D vector from 2D or 3D seed
vec2 random2(vec2 st) {
st = vec2(
dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3))
);
return fract(sin(st)*43758.5453123);
}
vec2 random2(vec3 st){
vec2 S = vec2(
dot(st,vec3(127.1,311.7,783.089)),
dot(st,vec3(269.5,183.3,173.542))
);
return fract(sin(S)*43758.5453123);
}
// A uniform (pseudo-)random from unit sphere from a seed
vec3 random_direction(vec3 seed) {
vec2 r2 = random2(seed);
float z = 2.0 * r2.x - 1.0;
float a = r2.y * 2.0 * 3.1415926;
float r = sqrt(1.0 - z*z);
return vec3(z, r * cos(a), r * sin(a));
}
`
const smooth_step = `
vec3 smooth_step(vec3 f) {
return f * f * (3.0 - 2.0 * f);
}
`
const improved_smooth_step = `
vec3 smooth_step( vec3 f) {
return 6.0*f*f*f*f*f - 15.0*f*f*f*f + 10.0*f*f*f;
}
`
const perlin_noise = `
float perlin_noise(vec3 st) {
vec3 i = floor(st);
vec3 f = fract(st);
vec3 u = smooth_step(f);
float dotgrad000 = dot(random_direction(i + vec3(0.0, 0.0, 0.0)), f - vec3(0.0, 0.0, 0.0));
float dotgrad001 = dot(random_direction(i + vec3(0.0, 0.0, 1.0)), f - vec3(0.0, 0.0, 1.0));
float dotgrad010 = dot(random_direction(i + vec3(0.0, 1.0, 0.0)), f - vec3(0.0, 1.0, 0.0));
float dotgrad011 = dot(random_direction(i + vec3(0.0, 1.0, 1.0)), f - vec3(0.0, 1.0, 1.0));
float dotgrad100 = dot(random_direction(i + vec3(1.0, 0.0, 0.0)), f - vec3(1.0, 0.0, 0.0));
float dotgrad101 = dot(random_direction(i + vec3(1.0, 0.0, 1.0)), f - vec3(1.0, 0.0, 1.0));
float dotgrad110 = dot(random_direction(i + vec3(1.0, 1.0, 0.0)), f - vec3(1.0, 1.0, 0.0));
float dotgrad111 = dot(random_direction(i + vec3(1.0, 1.0, 1.0)), f - vec3(1.0, 1.0, 1.0));
float x00 = mix(dotgrad000, dotgrad100, u.x);
float x01 = mix(dotgrad001, dotgrad101, u.x);
float x10 = mix(dotgrad010, dotgrad110, u.x);
float x11 = mix(dotgrad011, dotgrad111, u.x);
float xy0 = mix(x00, x10, u.y);
float xy1 = mix(x01, x11, u.y);
return mix(xy0, xy1, u.z);
}
`
const bump = random_direction + improved_smooth_step + perlin_noise + `
float smooth_heaviside( float x, float t) {
return (1./(1.+exp(-2.*t*(x)))-1./2.)/(1./(1.+exp(-2.*t*1.))-1./2.);
}
float bump_height(float is_moon, vec3 s) {
float b =
0.05 *(0.5+0.5 * smooth_heaviside(perlin_noise(1.0 * s), 10.0) * 2.0 - 1.0)
+(0.5 + 0.44*(1.0 - is_moon)) * (0.5 + 0.5 *smooth_heaviside((
+(0.6+0.14*is_moon)*perlin_noise(2.0*s)
+(0.2-0.04*is_moon)*perlin_noise(4.0*s)
),8.0-is_moon*-s.x*7.0)*2.0-1.0)
+0.01*(0.5+0.5*smooth_heaviside((
+0.1*perlin_noise( 16.0*s)
),4.0)*2.0-1.0)
-.5;
return 0.06*b+0.07;
}
vec3 bump_position(float is_moon , vec3 s) {
float bump = bump_height(is_moon, s);
vec3 p = s;
vec3 n = s;
return p + 1.0*bump*n;
}
void tangent(in vec3 N, out vec3 T, out vec3 B) {
vec3 x = vec3(1,0,0);
T = normalize(x-dot(N,x)*N);
B = cross(N,T);
}
`
const vertexShaders = {};
vertexShaders.simpleVertexShader = `
varying vec3 vNormal;
varying vec3 vPos;
varying vec3 vViewPos;
void main() {
vPos = position;
vViewPos = (modelViewMatrix * vec4(position, 1.0)).xyz;
vNormal = normalMatrix * normalize(normal);
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);;
}
`
const fragmentShaders = {};
fragmentShaders.normalFragmentShader = `
varying vec3 vNormal;
void main() {
gl_FragColor = vec4(0.5 + 0.5 * vNormal, 1.0);
}
`
fragmentShaders.posFragmentShader = `
varying vec3 vViewPos;
void main() {
vec3 color = vec3(0.5,0.5,0)+vec3(0.5,0.5,0)*vViewPos.xyz;
gl_FragColor = vec4(color, 1.0);
}
`
fragmentShaders.depthFragmentShader = `
varying vec3 vViewPos;
void main() {
vec3 color = (1.0+(vViewPos.z - -3.0)/5.0)*vec3(1.0,1.0,1.0);
gl_FragColor = vec4(color, 1.0);
}
`
fragmentShaders.phongFragmentShader = blinn_phong + `
uniform float is_moon;
uniform float time;
varying vec3 vPos;
varying vec3 vNormal;
varying vec3 vViewPos;
void main() {
vec3 l = mat3(viewMatrix) * normalize(vec3(1, -1, -1));
vec3 n = normalize(vNormal);
vec3 v = normalize(-vViewPos);
vec3 color = mix(vec3(0.9,0.2,0.3), vec3(0.5,0.45,0.5), is_moon);
vec3 fragColor = blinn_phong(
color, color, vec3(1.0, 1.0, 1.0), 300.0,
n, v, l
);
gl_FragColor = vec4(fragColor, 1.0);
}
`
fragmentShaders.perlinFragmentShader = blinn_phong + random_direction + smooth_step + perlin_noise + `
uniform float is_moon;
uniform float time;
varying vec3 vPos;
varying vec3 vNormal;
varying vec3 vViewPos;
void main() {
vec3 l = mat3(viewMatrix) * normalize(vec3(1, -1, -1));
vec3 n = normalize(vNormal);
vec3 v = normalize(-vViewPos);
vec3 color = mix(vec3(0.9,0.2,0.3), vec3(0.5,0.45,0.5), is_moon);
vec3 sphere_fs_in = normalize(vPos);
float s = sin(5.0*(sphere_fs_in.y + 0.5 *perlin_noise( sphere_fs_in ))) * (0.991+0.009*perlin_noise( 2.0 * sphere_fs_in));
float s2 = 0.25*perlin_noise( 1.0 * sphere_fs_in )
+ 0.25*perlin_noise( 4.0 * sphere_fs_in )
+ 0.25*perlin_noise( 8.0 * sphere_fs_in )
+ 0.25*perlin_noise(16.0 * sphere_fs_in );
float s3 = max(s+0.4,0.0) * pow(min((0.5+0.5*(
(0.2*sin(10.0*(sphere_fs_in.x + perlin_noise( 8.0*sphere_fs_in )))
+ 0.2*sin(15.0*(sphere_fs_in.z + perlin_noise( 8.0*sphere_fs_in )))
+ 0.2*perlin_noise(16.0*sphere_fs_in))
+ 0.6*perlin_noise(32.0*sphere_fs_in)
))
,1.0),2.0);
float b = 1.0-clamp(0.1*pow(s*0.5+0.5,20.0) + 0.7*(0.5*s2+0.5) + 0.2*s3, 0.0, 1.0);
color = blinn_phong(
b * color, b * color, vec3(1.0, 1.0, 1.0), 300.0,
n, v, l
);
gl_FragColor = vec4(color, 1.0);
}
`
fragmentShaders.bumpFragmentShader = blinn_phong + bump + `
uniform float is_moon;
uniform float time;
uniform mat3 normalMatrix;
varying vec3 vPos;
varying vec3 vNormal;
varying vec3 vViewPos;
void main() {
vec3 sphere_fs_in = vPos;
vec3 l = mat3(viewMatrix) * normalize(vec3(1, -1, -1));
vec3 n = sphere_fs_in;
vec3 v = normalize(-vViewPos);
vec3 color = mix(vec3(0.9,0.2,0.3), vec3(0.5,0.45,0.5), is_moon);
float s = sin(5.0*(sphere_fs_in.y + 0.5 *perlin_noise( sphere_fs_in )))
* (0.991+0.009*perlin_noise( 2.0 * sphere_fs_in));
float s2 = 0.25*perlin_noise( 1.0 * sphere_fs_in )
+ 0.25*perlin_noise( 4.0 * sphere_fs_in )
+ 0.25*perlin_noise( 8.0 * sphere_fs_in )
+ 0.25*perlin_noise(16.0 * sphere_fs_in );
float s3 = max(s+0.4,0.0) * pow(min((0.5+0.5*(
(0.2*sin(10.0*(sphere_fs_in.x + perlin_noise( 8.0*sphere_fs_in )))
+ 0.2*sin(15.0*(sphere_fs_in.z + perlin_noise( 8.0*sphere_fs_in )))
+ 0.2*perlin_noise(16.0*sphere_fs_in))
+ 0.6*perlin_noise(32.0*sphere_fs_in)
))
,1.0),2.0);
float b = 1.0-clamp(0.1*pow(s*0.5+0.5,20.0) + 0.7*(0.5*s2+0.5) + 0.2*s3, 0.0, 1.0);
vec3 bp = bump_position(is_moon, sphere_fs_in);
float eps = 0.0001;
vec3 T;
vec3 B;
tangent(n,T,B);
vec3 pT = sphere_fs_in+eps*T;
vec3 pB = sphere_fs_in+eps*B;
n = normalize(cross(
bump_position(is_moon, pT)-bp,
bump_position(is_moon, pB)-bp));
n = normalMatrix * normalize(n);
color = blinn_phong(
b * color, b * color, vec3(1.0, 1.0, 1.0), 300.0,
n, v, l
);
gl_FragColor = vec4(color, 1.0);
}
`
export { vertexShaders, fragmentShaders };