Approxmation Errors and Conditioning, Stability

import matplotlib.pyplot as plt
import numpy as np

Let \(A:=\) approximation, \(T:=\) true value

Absolute error and relative error

Absolute error \(A-T\)
Relative error \(\frac{A-T}{T}\), let \(A-T = \delta\), then \(A = T(1+\delta)\) avoids the issue with \(A = 0\)

Connect Digits \(A:= 5.46729 \times 10^{-12}, T:= 5.46417\times 10^{-12}\)
Then, \(\delta_{absolute}= A-T = 0.000312 \times 10^{-12}\)
\(\delta_{relative} = 0.000312 / 5.46417 = 3.12/5.46417 \times 10^{-3}\)
Let \(p\) be the first non-agreed digit, then the magnitude relative error will be around \(10^{-p\pm 1}\).

0.99... = 1 However, consider \(A= 1.00596\times 10^{-10}, T = 0.99452 \times 10^{-10}\), the relative error is much smaller than the magnitude approximation. Therefore, we say that \(0.999...\) agrees with \(1.000...\), hence \(A,T\) agrees on 2 sig digits.

Data error and computational error

Data error let \(\hat x:=\) input value, \(x\) be actual value, error = \(\hat x - x\), for example - we cannot represent \(A\) as a terminating floating number \((3.14\sim \pi)\) - measurement error

Computational error let \(f\) be the actual mapping, \(\hat f\) be the approximation function, errors of the computation is \(\hat f(x) - f(x)\), for example - often \(\cos\) is calculated by its Taylor series, while Taylor series is a infinite sum, and we can only compute by finite approximation.

Truncation error and rounding error (subclasses of computational error)

Truncation error The difference between the true result \(f\) and the result that would be produced by a given (finite approximation) algorithm using exact arithmetic \(\hat f\).

rounding error The difference between the result produced by a given algorithm using exact arithmetic, and the result produced by the same algorithm using a finite-precision, rounded arithmetic.

Example To approximate \(f'(x)\) with known \(f\)
By definition \(f'(x) = \lim_{h\rightarrow 0} \frac{f(x+h) - f(x)}{h}\), hence, choose a small but not necessarily 0 value \(h\), we can approximate \(f'(x)\) for all \(x\).
Assuming \(f\) is smooth, then

Therefore, the truncation error will be \(\frac{f''(c)h}{2}\), by IVT, such error is bounded since \(f\) is continuous.

Then, let \(FL\) be the mapping to the floating representation result, assume

Note that \(\epsilon_h\) is less influenced by \(h\) when \(h\) is small, then we can looks \(\epsilon_h -\epsilon_0 =:\epsilon\) as a constant.
Then, let \(E(h)\) be the total error, \(E'(h) = f''(c)/2 - \frac{\epsilon}{h^2}\Rightarrow argmin(E(h))=\sqrt{\epsilon_h/M}\)

Claim \(\lim_{h\rightarrow 0} FL(f(x+h)) - FL(f(x)) = 0\)

Notice that when \(h\) is particularly smaller than the machine's precision, i.e. \(x>>h\), then \(x + h\) will be exactly \(x\).

Therefore, for very small \(h\), \(FL\bigg(\frac{f(x+h) - f(x)}{h} -f'(x)\bigg) = FL(-f'(x))\)

Forward Error and backward error

Let \(y = f(x)\) be the true result, \(\hat y = COMP(f(x))\) be the computational result, where \(COMP\) is all the possible errors caused in the computation. Then, forward error is \(\hat y - y\).
Take \(\hat x\) such that with the true computation, \(\hat y = f(\hat x)\), then backward error is \(\hat x - x\)

Conditioning of Problems

Let \(\hat x \in (x-\delta, x+\delta)\), i.e. any \(\hat x\) within the neighborhood of some \(x\).
Consider the relative forward error, assume \(f\) is differentiable around \(x\)

The problem is well conditioned if \(\forall x\), condition number is small; is ill conditioned if \(\exists x\), condition number is large

Connection to Approximation error \(y = f(x) \Rightarrow \hat y = f(\hat x)\), \(\hat x - x\) will have different conditioning with \(\frac{\hat x- x}{x}\), often we measuring the relative errors

Example \(f(x):= \sqrt x, x\geq 0\)
\(\forall x \geq 0. c\approx\frac{xf'(x)}{f(x)} = \frac{x}{2\sqrt x\sqrt x} = 1/2\Rightarrow\) very well-conditioned

Example \(f(x)=e^x\)

\(c\approx \frac{xe^x}{e^x} =x\Rightarrow\) less and less well-conditioned when \(x\) gets big. However, \(e^x\) will overflows or underflows if \(|x|\) is large, even before it gets ill-conditioned.

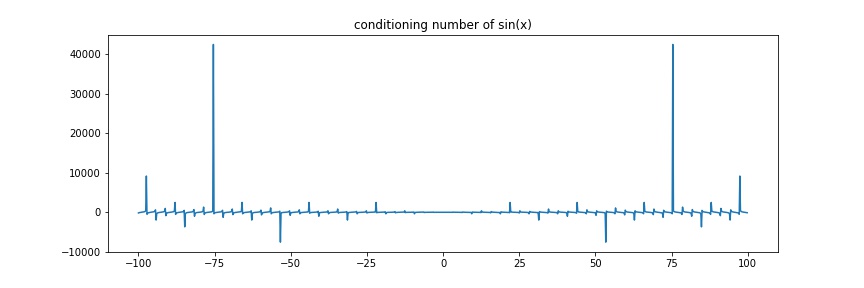
Example \(f(x)=\sin(x)\)

\(c\approx \frac{x\cos(x)}{\sin(x)} = x\cot(x)\Rightarrow\) ill-conditioned near \(k\pi, k\neq 0\) or \(|x|\) is big and \(\cos(x)\neq 0\)

t = np.arange(-5., 5., 0.01)
plt.figure(figsize=(12, 4))
plt.plot(t, t * np.cos(t) / np.sin(t))
plt.title("conditioning number of sin(x)")
plt.savefig("assets/approx_error_1.jpg")

t = np.arange(-100., 100., 0.2)
plt.figure(figsize=(12, 4))
plt.plot(t, t * np.cos(t) / np.sin(t))
plt.title("conditioning number of sin(x)")
plt.savefig("assets/approx_error_2.jpg")

Stability of Algorithms

An algorithm is stable if small change to the input results in small change in the output

stable ≠ good

Consider \(\hat f(x) := 0\: vs. f(x):= \sin(x)\), it is very stable, while it does not accomplish a good approximation as wanted.