k-Means and EM Algorithm
Clustering Problem
Grouping data points into clusters, without observed labels.
Samples within a cluster are similar to each other, and samples in different clusters are dissimilar. Such data forms a multimodal distribution, as having multiple modes.
K-Means
Given data points \(x^{(1)},...,x^{(N)}\in \mathbb R^D\), want to find cluster centers \(\{m_k\}^K\in\mathbb R^D\) and assignments \(\{r^{(n)}\}^N\in \mathbb R^K\) being 1-K encoding.
The objective is to minimize the cost as the squared sum distance of data points to their assigned centers, i.e.
Because \(r\) works as an encoding, i.e. integer optimization problem, optimize both \(r,m\) will be NP-hard.
However, if we fix \(m\), finding optimal assignments \(r\) is easy, i.e.
If we fix \(r\), then we can minimize by taking gradient and set to 0
Therefore, it is possible to do alternating minimization, i.e. minimize \(J\) w.r.t. \(m, k\) individually .
Alternating Minimization Algorithm
- Initialize with random cluster centers
- For each iterative step
- Assignment step: assign data point to closest cluster by nearest neighbor
- Refitting step: move each cluster center to the mean of the data assigned to it.
Convergence
Note that \(J\) is lower bounded by 0 as a squared distance.
Also, consider each assignment step, as \(m\) fixed, for each \(x^{(n)}\), \(r_k^{(n)}\) guarantees \(x^{(n)}-m_k\) is minimum.
Consider each minimization step, as \(r\) fixed, for each \(\sum r_k( x^{(n)} - E(x^{(n)}))^2\) is minimized.
Therefore, by monotone convergence theorem, this will converge.
However, this will not guarantee the global minimum.
Soft k-Means
Instead of making 0-1, we can make soft assignment, which we assign the clusters by responsibility (probability).
Algorithm
- Initialize \(m\) random
-
Iterative step
- Assignment
\[r_k^{(n)} = \frac{\exp(-\beta\|m_k-x^{(n)}\|^2)}{\sum_j\exp (-\beta \|m_j-x^{(n)}\|^2)} = softmax(-\beta\{\|m_k-x^{(n)}\|^2\}^K)\]- Refitting
\[m_k = \frac{\sum_n r_k^{(n)}x^{(n)}}{\sum_n r_k^{(n)}}\]
Note that
\((*)\) when \(k\) is the argmin, then \(d:=\|m_j-x^{(n)}\|^2 - \|m_k-x^{(n)}\|^2 > 0, -\beta d\rightarrow -\infty, \exp(-\beta d)\rightarrow 0\).
Otherwise, exists some \(d<0, \exp(-\beta d) \rightarrow \infty, \lim r^{(n)}_k = 0\)
However, this raises questions about how to set \(\beta\), and how to cluster unequal weight and width.
Termination condition
We can test whether we can terminate the k-Mean's iterative steps by checking whether the assignment change.
Generative Model
Consider the generative model for \(\mathcal D\):
Assume data point \(x\) is generated as - choose a cluster \(z\) from \(\pi = [\pi_1,...,\pi_K]^T, p(z=k)=\pi_k\) - Given \(z\), sample \(x\) from \(N(x|\mu_z, I)\)
Then the joint distribution \(p(z,x) = p(z)p(x|z)\) with parameters \(\{\pi_k, \mu_k\}^K\), marginal probability of \(x, p(x)=\sum_zp(z,x)\)
the probability \(x\) came from kth cluster is \(p(z=k|x) = \frac{p(x|z=k)p(z=l)}{p(x)}\)
Gaussian Mixture Model (GMM)
Using MLE approach, since we can't see the cluster assignments \(z\), we only see \(x\), i.e. the pbjective is
Such distribution is an example of Gaussian Mixture Model (GMM) and \(\pi_k\) are the mixing coefficients.
In general, each Gaussian will have different covariance, i.e. \(N(x|\mu_k, \sigma_k)\).
Note that \(\log(p(\mathcal D)) = \sum^N\log \bigg(\sum^K \pi_k N(x^{(n)}| \mu_k, I)\bigg)\)
Similar to k-Means, if we knew \(z^{(n)}\), i.e. assignment, then the log likelihood is similar to a classification question, i.e.
The maximization results in
Then, we replace assignment since \(E(z^{(n)}) = p(z=k|x)\) where \(p(z=k|x)\) is computed from Bayes rule
Therefore, let \(r_k^{(n)} := p(z^{(n)}=k|x^{(n)})\) replace \(\mathbb I(z^{(n)}=k)\), and
The maximization results in
Expectation Maximization Algorithm
- E-step compute the posterior probabilities \(r_k^{(n)} = p(z^{(n)}=k|x^{(n)})\) given our current model
- M-step update \(\mu, \pi\)
Possible Problems
- Singularities: arbitrarily large likelihood when a Gaussian explains a single point with variance shrinking to zero
- Non-convex
Source code
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
import scipy as sp
# --8<-- [start:kmeans]
def kMeans(x, k, step, m=None):
# initialization
if m is None:
m = x[np.random.choice(x.shape[0], k)]
# iterative step
for i in range(step):
# assignment step
kd = sp.spatial.KDTree(m)
r = kd.query(x)[1]
# refitting step
for c in range(k):
m[c] = x[r == c].mean(axis=0)
return r, m
# --8<-- [end:kmeans]
size = 3
centers = np.random.uniform(-5, 5, (size, 2))
sds = np.random.uniform(0.8, 1, size)
x, t = make_blobs(n_samples=500, centers=centers, n_features=2, cluster_std = sds, random_state=0)
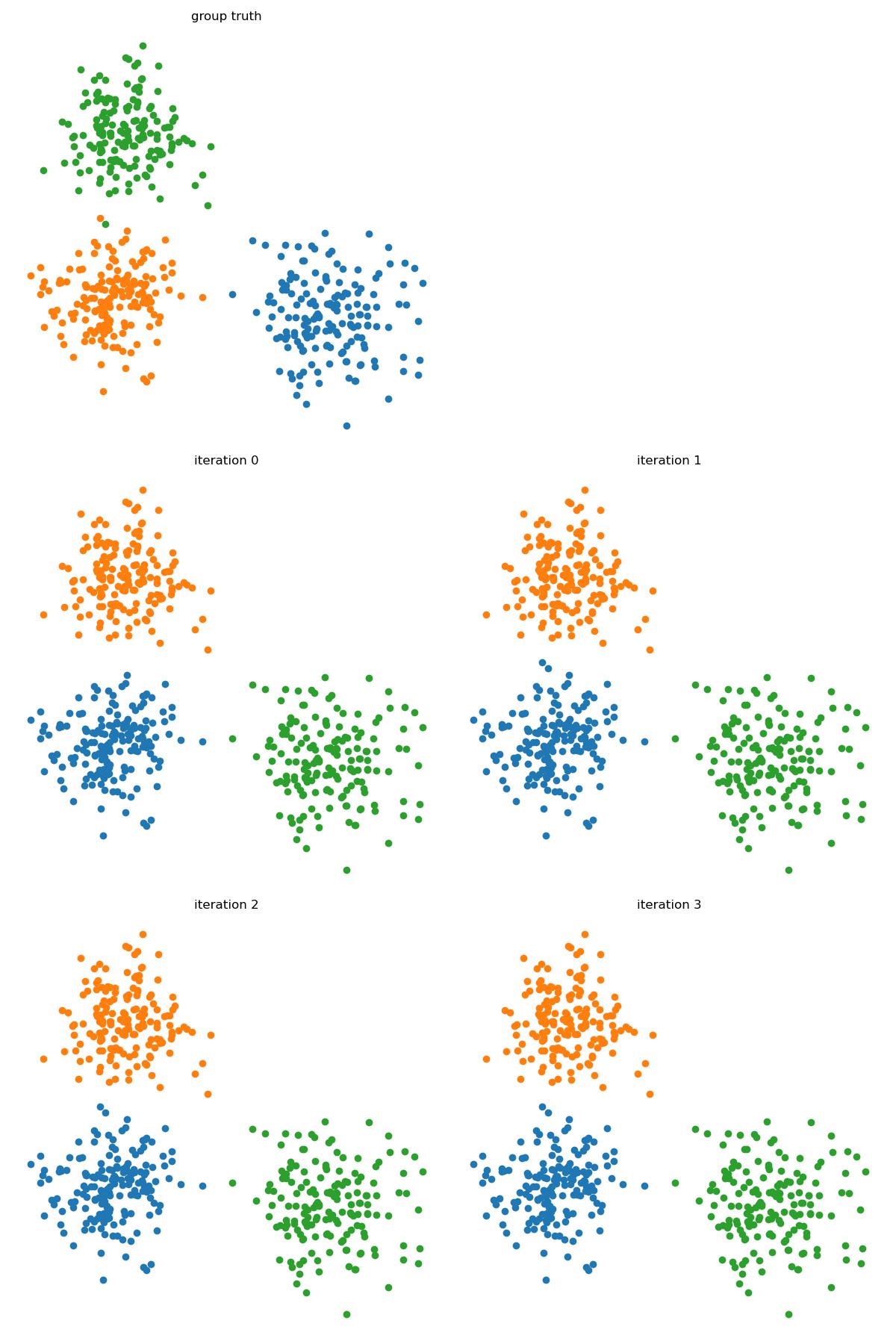
plt.figure(figsize=(12, 18))
plt.subplot(321)
for i in range(size):
plt.scatter(x[t==i, 0], x[t==i, 1])
plt.title("group truth")
plt.axis("off");
r, m = kMeans(x, 3, 1)
for iteration in range(4):
plt.subplot(3, 2, 3 + iteration)
plt.title("iteration " + str(iteration))
plt.axis("off");
for i in range(r.max() + 1):
plt.scatter(x[r==i, 0], x[r==i, 1])
r, m = kMeans(x, 3, 1, m)
plt.tight_layout()
plt.savefig("../assets/kmeans_1.jpg")
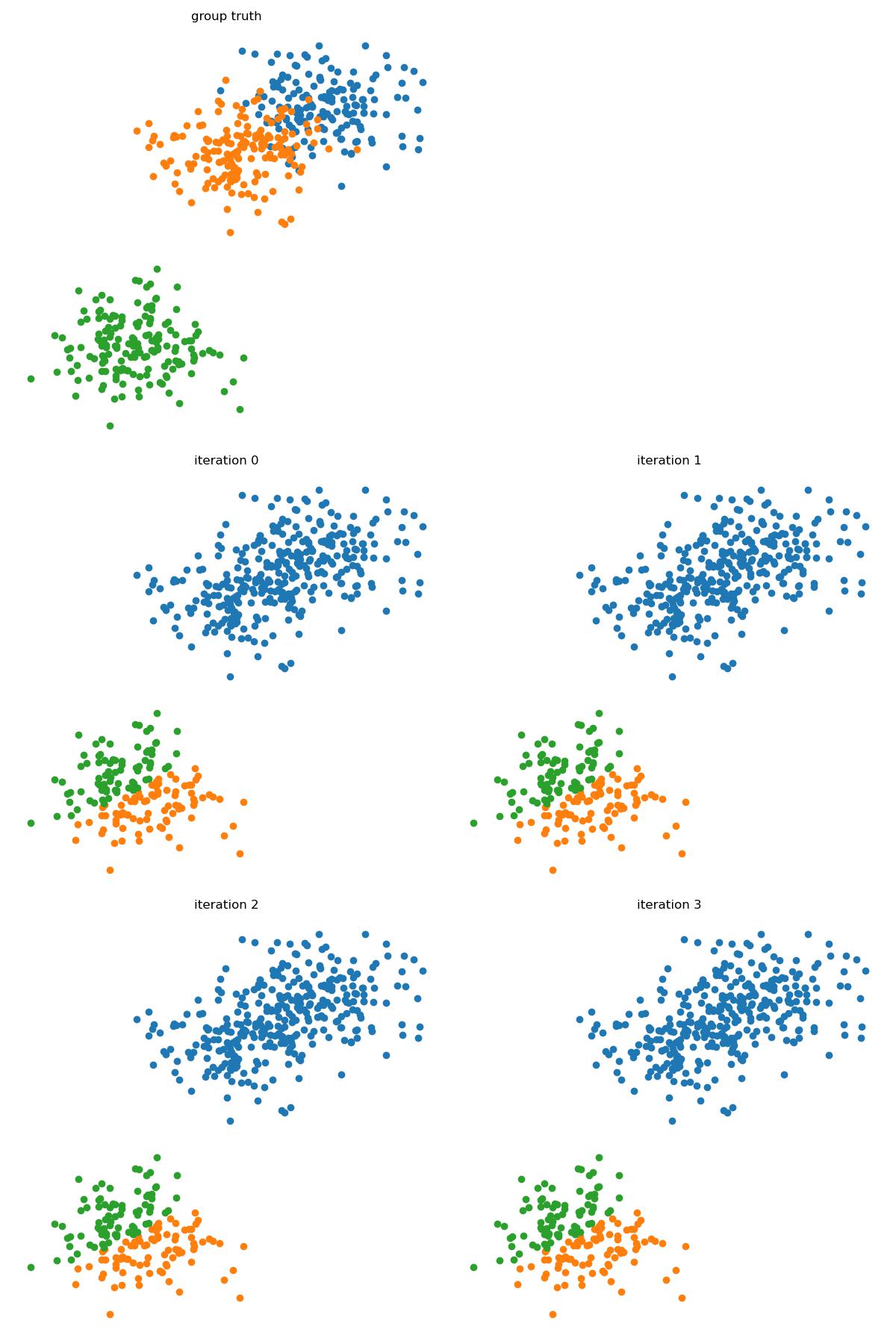
centers = np.array([[ 1.69653073, 4.85908807], [ 0.13447474, 3.7240316 ], [-2.02381919, -2.05536678]])
sds = 0.8119142178109643
m = np.array([[ 0.84192262, 4.26238333], [-1.67684624, -2.56679316], [-2.44040286, -1.48432092]])
x, t = make_blobs(n_samples=500, centers=centers, n_features=2, cluster_std = sds, random_state=0)
plt.figure(figsize=(12, 18))
plt.subplot(321)
for i in range(size):
plt.scatter(x[t==i, 0], x[t==i, 1])
plt.title("group truth")
plt.axis("off");
r, m = kMeans(x, 3, 1, m)
for iteration in range(4):
plt.subplot(3, 2, 3 + iteration)
plt.title("iteration " + str(iteration))
plt.axis("off");
for i in range(r.max() + 1):
plt.scatter(x[r==i, 0], x[r==i, 1])
r, m = kMeans(x, 3, 1, m)
plt.tight_layout()
plt.savefig("../assets/kmeans_2.jpg")