Priority Queue: Max Heap

Abstract Data Type

• Object:
  • Set \(S\) of keys (integers) and values
• Operations:
  • peek() return the element of \(S\) with the highest priority
  • pull() return highest priority and removes it from \(S\)
  • insert(key, value) add key, value to \(S\)

Data Structure: Max(Min) Heap

Max heap, as the data structure, is a implementament of priority queue.

Object:

• A complete binary tree \(T\) of size \(n\) where the key of every node is at least the keys of its children.
• By "complete", every level is full except possibly the last one where all nodes are fully to the left.
• Note that, since \(T\) is complete, we can store it as an array instead of a tree object.

Claim 1 The max level of a complete binary tree with \(n\) nodes is \(\lfloor\lg n\rfloor\)

proof. Consider the number of nodes for a complete binary tree with height \(h\)

where the lower bound is the tree with 1 leaf at \(h\) level, and upper bound will have \(2^h\) leaves at \(h\) level.

Thus, \(h = \lfloor\lg n\rfloor\)

Observation We can map a complete binary tree to an array via - \(\text{root} = 0\) - \(\text{parent}(i) = \lfloor i / 2\rfloor\) - \(\text{left}(i) = 2i + 1\) - \(\text{right}(i) = 2i + 2\)

Operations

• max() return the root of the tree.
• insert(x) put \(x\) in the leftmost position of the leaf level, then swap with its parent if it is smaller than its parent.
• extract_max() remove the root, move the leftmost to the root. Swap with its larger child till it's large than its children.

Heapify

The swap operation can be considered as a structural induction heapify(A, i)

• precondition: left and right subtree of \(A[i]\) are both heap.
• postcondition: The tree rooted at \(A[i]\) is a heap.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

l = left(i)
r = right(i)
largest = i
if i has left child and A[l] > A[largest]:
    largest = l
if i has right child and A[r] > A[largest]:
    largest = r
if largest != i:
    swap(A[i], A[largest])
    max_heapify(A, largest)

Correctness

Base case: - \(H[i]\) is a leaf, then it is a heap.

Induction Step:

• If \(A[i]\) does not violate max heap property, meaning it is larger than or equal to both children. Then none of the if conditions are satisfied and we are done.
• If \(A[i]\) is smaller than any of its children, than by line 4-7, largest will be set to the index of the larger child. By line 8-10, WLOG assume that largest = r. Then, after the swap
  • Left subtree is untouched, by precondition, it is a max heap.
  • Right subtree is a max heap by line 10 and induction hypothesis.
  • The new root, by line 4-9, is greater than or equal to its children.

Runtime

Each time, a swap happens between a parent and child, in the worst case, we swap from root to a leaf, by Claim 1, resulting \(T(n) \in O(h)\).

Build Heap from Array

1
2
3

n = len(A)
for i in [floor(n / 2): 0: -1]:
    max_heapify(A, i)

Correctness

Consider the for loop, we want to prove the loop invariance that the tree rooted at \(A[i]\) is a max heap.

For \(i = \lfloor n / 2\rfloor\). Note that \(h = \lfloor \lg n\rfloor\), thus the node is in the second last level. It subtrees are either leaf or empty, hence by correctness of max_heapify, the loop invariance is met.

For \(i < \lfloor n / 2\rfloor\), by loop counter, since \(\text{left}(i) = 2i + 1 > i, \text{right}(i) = 2i+2 > i\), both subtrees either empty or have already run max_heapify, thus, the loop invariance is met.

Runtime

Claim \(T(n)\in O(n)\) Consider the for loop, at each height \(h\), there are at most \(n/2^h\) nodes, and each max_heapify takes \(O(h) = ch\) time. Therefore,

Note that by Maclaurin series

Therefore, we have that

Heap Sort

Given an array, return a sorted array using the heap

1
2
3
4
5

H = build_heap(A)
sorted = []
for i in [0:n:1]:
    sorted.append(extract_max(H))
return sorted

Correctness is trivial, since \(H\) is a heap and we always extract the largest element.

Runtime: line 1 takes \(O(n)\), the for loop in line 3-4 takes \(n \times O(h) \in O(n \lg n)\). Thus, \(T(n) \in O(n\lg n)\).

Implementation

class PriorityQueue:
    def __init__(self, arr):
        """ Create a priority queue from a given 
            list of priorities
        """
        raise NotImplementedError

    def peek(self):
        """ return the highest priority
        """
        raise NotImplementedError

    def pull(self):
        """ return the highest priority and extract it
        """
        raise NotImplementedError

    def insert(self, priority):
        """ insert a priority 
        """
        raise NotImplementedError

from .priority_queue import PriorityQueue

class Heap(PriorityQueue):
    def __init__(self, arr, ascending=False):
        self.H = arr
        if ascending:
            self.compare = lambda x, y: x < y
        else:
            self.compare = lambda x, y: x > y
        for i in range(len(arr) // 2, -1, -1):
            self.__heapify(i)


    @staticmethod
    def left(i):
        "given the index, return the index of left child"
        return 2 * i + 1

    @staticmethod
    def right(i):
        "given the index, return the index of right child"
        return 2 * i + 2

    @staticmethod
    def parent(i):
        "given the index, return the index of parent"
        return (i - 1)// 2

    def __heapify(self, i):
        """ Given the complete binary tree H and index i, 
            assume that the left subtree and right subtree of 
            of H[i] are max-heap.
            make H a max heap
        """
        largest = i
        l, r = Heap.left(i), Heap.right(i)
        if l < len(self.H) and self.compare(self.H[l], self.H[largest]):
            largest = l
        if r < len(self.H) and self.compare(self.H[r], self.H[largest]):
            largest = r
        if largest != i:
            self.H[i], self.H[largest] = self.H[largest], self.H[i]
            self.__heapify(largest)

    def peek(self):
        return self.H[0]

    def pull(self):
        m = self.H[0]
        self.H[0] = self.H[-1]
        self.H.pop()
        self.__heapify(0)
        return m

    def insert(self, x):
        self.H.append(x)
        i = len(self.H) - 1
        while self.compare(self.H[i], self.H[Heap.parent(i)]) and i != 0:
            self.H[i], self.H[Heap.parent(i)] = self.H[Heap.parent(i)], self.H[i]
            i = Heap.parent(i)

    def plot(self, path):
        from .plot_trees import TreeNode, plot_tree
        if len(self.H) == 0:
            return
        nodes = [TreeNode(str(self.H[0]))]
        for i in range(1, len(self.H)):
            new_node = TreeNode(str(self.H[i]), nodes[Heap.parent(i)])
            nodes.append(new_node)
            nodes[Heap.parent(i)].children.append(new_node)

        return plot_tree(nodes[0], path)

def heap_sort(arr, ascending=False):
    H = Heap(arr, ascending=ascending)
    sorted = []
    for _ in range(len(arr)):
        sorted.append(H.pull())
    return sorted

from assets.heap import Heap, heap_sort

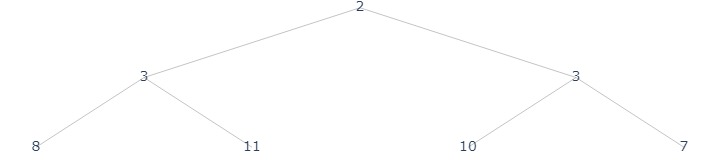
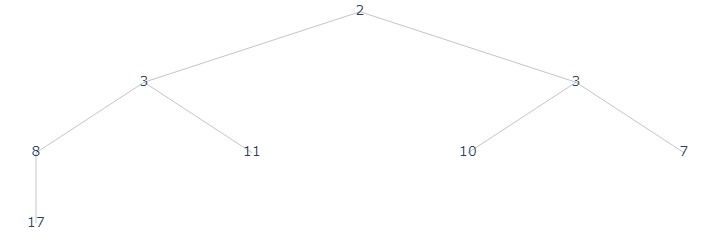
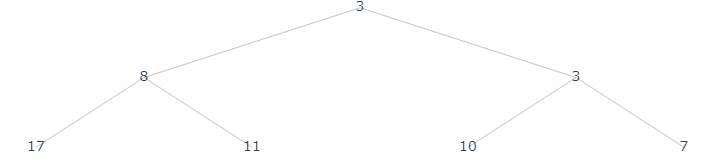
arr = [2, 11, 10, 8, 3, 3, 7]
# ascending = True => min heap
# ascending = False => max heap
# default max heap
h = Heap(arr, ascending=True)
h.plot("./assets/pq_0.jpg")

h.insert(17)
h.plot("./assets/pq_1.jpg")

print(f"{h.pull()}")
#>> 2

h.plot("./assets/pq_2.jpg")

print(f"> {h.pull()}")
#>> 3

h.plot("./assets/pq_3.jpg")

print(f"> {heap_sort(arr)}")
#>>  [17, 11, 10, 8, 7, 3]

[+] Usage Example

Given a sorted array \(A\) of distinct integers of length \(n > 1\). Design a data structure that supports - perprocess(A) initialize the data structure. This operation should run in \(O(n)\) - next(A) return the next pair \((i,j), 1\leq i\leq j\leq n\) in non-decreasing order \(A[j] - A[i]\). Each call should run in \(O(\log n)\)

We can assume that preprocess is called once, following at most \(n\choose 2\) calls to next.

Observations

Lemma 1 Let \((i_i, j_i)\) be the return value of the ith call to next. Then, \(j_1 - i_1 = 1, j_2 - i_2 = 1\).
proof. Since \(A\) is sorted. If \(j_1 - i-1 > 1\), then there exists \(A[j_1 - 1] - A[i_1] < A[j_1] - A[i_1]\).
Moreover, consider \((i_2, j_2)\), \(A[j_2] - A[i_2 + 1] < A[j_2] - A[i_2]\).

Lemma 2 Let \(\sigma = [(i_1, j_1),...,(i_N, j_N)]\) be the sequence of return values from \(N = {n\choose 2}\) calls of next. Then for any \(k\), either \(j_k - i_k = 1\) or \((i_k, i_{k+1})\) and \((i_{k+1},j_k)\) appear before \((i_k,j_k)\) in \(\sigma\).

Implementataion

 1  L = [ ( A[i+1] - A[i], (i, i+1) ) for i in [0: n-1: 1] ]
 2  return build_min_heap(L)

 1  (i, j) = extract_min(A)
 2  if i > 0:
 3      insert(A[j] - A[i-1], (i-1, j))
 4  return (i, j)

Analysis

Runtime analysis is trivial.

For correctness,

Claim 1 each pair \((i,j)\) inserted is distinct. proof. For pairs inserted in preprocess this is obvious. For any pair inserted in next, we must have that \(j-i > 1\), considering line 3. Suppose that \((i,j)\) is the first pair that got inserted twice, then it must exists \((i, j-1)\) be extracted twice, meaning it is inserted before, contradiction.

Claim 2 For each \((i_k, j_k)\), \(A[j_k] - A[i_k]\) is the \(k\)th smallest.
proof. For \(k = 1\), by lemma 1 this is proven. Then, assume \(k>1\) is the first step where \(A[j_k] - A[i_k]\) is not minimal. Let \((i,j)\) be the pair that should be extracted at \(k\)th step, \((i,j)\neq (i_k, j_k), A[j]-A[i] < A[j_k] - A[i_k]\). Note that \(j - i > 1\), otherwise it is inserted through preprocess and must be extracted. Then, for \(j - i > 1\), then by lemma 2, \((i+1, j)\) must have been extracted. Therefore \((i,j)\) must have been inserted. By the property of heap, \((i,j)\) must be extracted at \(k\)th step.