Skip to content

Disjoint Set

ADT: Disjoint Set

  • Objects: a collection of disjoint sets \(\mathcal S = \{S_1,..., S_k\}\) where each set has a representative \(x_i\in S_i\).
  • Operations:
    • makeset(x) If \(x\) is not already in any sets of \(\mathcal S\) (since disjoint), then create a new set of only \(\{x\}\) with representative \(x\). Otherwise return error.
    • findset(x) given a pointer to the element, return the representative of the set containing \(x\).
    • union(x, y) union the sets that contain \(x\in S_i, y\in S_j\), and choose any element within \(S_i\cup S_j\) to be the new representative. Note that x, y can be in the same set, in which union(x, y) should do nothing.
    • link(x, y) save as union, but with the precondition that x, y must be representatives of different sets.

Connected component

Connected components is a common problem in geometry processing. For graph \(G = (V, E)\). A connected component is a subset of vertices \(V' \subseteq V\) s.t. for any pair of vertices \(v_1, v_2 \in V'\), there exists a path between them. Thus, a graph can have several connected components.

With a disjoint set, we can let the vertices be the elements, then union two sets together if there is an edge.

connected_components(G)
1
2
3
4
5
for v in G.v:
    makeset(v)
for (u, v) in G.E:
    if findset(u) != findset(v):
    union(u, v)

from assets.disjointset import DisjointSet
from random import randint, seed


seed(21)
NV = 25
E = set()
while len(E) < NV * 2 // 3:
    x, y = randint(0, NV - 1), randint(0, NV - 1)
    if x != y and (y, x) not in E :
        E.add((x, y))
E = list(E)
label_fn = lambda x: f"{x.value}<br>{x.rank}"

import igraph as ig
import matplotlib.pyplot as plt

fig, ax = plt.subplots()
g = ig.Graph()
g.add_vertices(NV)
g.add_edges(E)
ig.plot(g, target=ax)
ax.set_axis_off()
fig.savefig("assets/disjoint_set_1.jpg")

png

Note that union(x, y) = if findset(x) != findset(y): link(findset(x), findset(y)). We use link to decompose the union operation so that the time analysis is directly related to the number of link and findset.

Claim 1 Define \(T(m, n), m \geq n\) be the worst case time executing any set of \(m\) operations from {makeset, findset, link}, which \(n\) of the operations are makeset, starting from \(\mathcal S = \emptyset\).
Then, there are at most \((n-1)\) link's. proof. There are at most \(n\) sets, and each link merges two sets into one, thus reduces the number of sets by \(1\).

Naive Implementation: Set of Trees / Linked lists

  • Objects: each set \(S_i\) is stored as a trees, where the representative is the root of the tree. Then, we store all roots in a list.
  • Operation:
    • makeset(x) make a new tree containing \(x\), and put into \(\mathcal S\). Taking \(O(1)\) time.
    • findset(x) recursively traverse the parent until the root. Takeing \(O(h)\) time where \(h\) is the height of the tree.
    • link(x, y) take one root and connected to another

Note that linked list is also a tree, and it's the simplest implementation of the disjoint set. However, the runtime for findset with linked list implementation will be \(O(n)\). In worst case, \(T(m,n) \in O(mn)\) which is far too large.

Another implementation is to have 2 level trees, where all nodes except the root are children of the root. In this case, findset(x) takes \(O(1)\) time, while link(x, y) need to reconnected all nodes in one set to another. Resulting \(T(m,n) \in O(mn)\) time again.

Therefore, we need to keep a good balance in between findset and link.

ds = DisjointSet()
for v in range(NV):
    ds.makeset(v)
nodes = ds.nodes
for e in E:
    ds.union_naive(nodes[e[0]], nodes[e[1]])
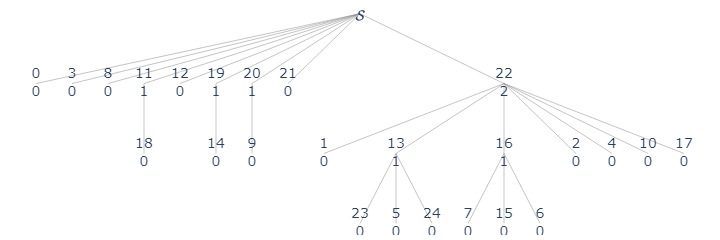
ds.plot(label_fn, "assets/disjoint_set_2.jpg")

png

Heuristic 1: Weighted Union

We want to make sure the tree height is small, while keeping link in \(O(1)\) time. Thus, the simplest idea is to attach the shorter tree to the root of the longer tree, thus the total height won't change. Thus, for each tree, we can store its height.

makeset(x)
1
2
x.height = 0
S.append(x)
link(x, y)
1
2
3
4
5
6
7
if x.height > y.height:
    y.parent = x
elif x.height < y.height:
    x.parent = y
else:
    y.parent = x
    x.height += 1

Time Analysis

Claim 2 After any operation on the disjoint set, for any element \(x \in S_i \in \mathcal S\), \(|S_i| \geq 2^{x.\text{height}}\).

proof. Note that only makeset and link will modify \(\mathcal S\). So that we will use induction on the operations.

For makeset, the other sets won't change, and the newly added set is \(\{x\}\) with height 0, and we have that \(2 \geq 2^0\).

For link(x, y), if their height is different, WLOG assume x.height > y.height so that \(S_x\) is merged into \(S_y\), and the size of the new set is \(|S_x| + |S_y| \geq 2^{x.\text{height}} + 2^{y.\text{height}} \geq 2^{y.\text{height}}\)

For link(x, y) with the same height, then the size of the new set is

\[|S_x| + |S_y| \geq 2^{x.\text{height}} + 2^{y.\text{height}} = 2^{x.\text{height} + 1}\]

Corollary 3 For any \(x\in S_x\in \mathcal S, x.\text{height} \leq \lfloor \lg n\rfloor\)

proof. from Claim 2 we have

\[\begin{align*} |S_x| &\geq 2^{x.\text{height} + 1}\\ n &\geq 2^{x.\text{height} + 1}\\ \lg n &\geq x.\text{height} + 1\\ \lfloor \lg n\rfloor &\geq x.\text{height}\\ \end{align*}\]

Corollary 4 \(T(m,n) \in O(m\log n)\)

ds = DisjointSet()
for v in range(NV):
    ds.makeset(v)
nodes = ds.nodes
for e in E:
    ds.union_weighted(nodes[e[0]], nodes[e[1]])
ds.plot(label_fn, "assets/disjoint_set_4.jpg")

png

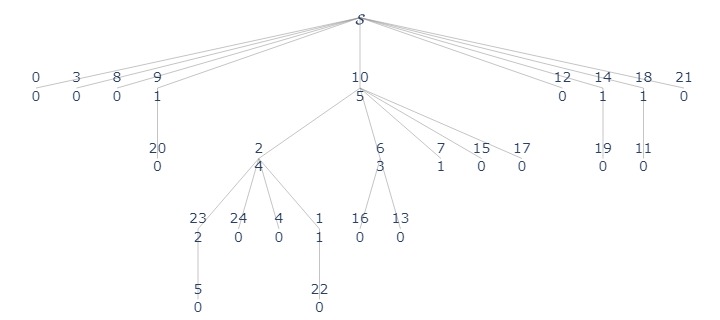
Heuristic 2: Path Compression

When we do findset, we have already put the effort in tracing the parent, we can, at the same time, update all nodes on the traced path directly point to the root.

findset(x)
if x.parent is None:
    return x
root = findset(x.parent)
x.parent = root
return root

ds = DisjointSet()
for v in range(NV):
    ds.makeset(v)
nodes = ds.nodes
for e in E:
    ds.union_compression(nodes[e[0]], nodes[e[1]])
ds.plot(label_fn, "assets/disjoint_set_5.jpg")

png

[+] Time Analysis (log-star)

Define the iterated logrithm \(\log^*\) as

\[\log_{b}^* n = \begin{cases}0 &n \in \{0, 1\}\\1+\log^*(\log n) &n>1\end{cases}\]

and its inverse function tetration

\[b\upuparrows n = \begin{cases}0 & n = 0\\b^{b\upuparrows n-1} &n>0\end{cases}\]

For convinence, assume that \(n\) is a power of \(2\), so that we don't have to deal with floors or ceilings.

Define find path be the sequence of nodes (and the edges connecting node and its parent) from a node \(u\), by recursively traversing its parent, to the root.

Lemma 1 The rank on a findset path is increasing.
proof. Since link, with weighted union, will always have higher rank nodes be the root. Then, findset will only attach to the root, while we have the assumption that all nodes has smaller rank than the root.

Lemma 2 The max number of nodes of rank \(r\) is at most \(\frac{n}{2^r}\).
proof. First note that in our algorithm, rank cannot decrease and rank only changes in link. Then, by weighted union, to make a node of rank \(r > 0\), you need at least two nodes of rank \(r-1\). Thus, recursively, you need at least \(2^r\) nodes to create a node of rank \(r\). And we have a total of \(n\) nodes.

Claim 3 (log-star runtime) \(T(m,n) \in O(m\log^* n)\)

proof. First, define the intervals \(b_0 = [0, 0], b_i = [(2\upuparrows {i-1}), (2\upuparrows {i}) - 1]\) for \(i = 1, 2, ...\) As some references, \(b_0 = [0, 0], b_1 = [1, 1], b_2 = [2, 3], b_3 = [4, 15], b_4 = [16, 65535]\).
Then we define the partition over \(\mathcal S\) as some "buckets"

\[B_i = \{x\in\mathcal S: x.\text{rank} \in b_i\}\]

We have the following claims:

  1. the total number of buckets is at most \(\log_2^* n\), as the inverse of tetration.
  2. the number of elements in bucket \([B, 2^B - 1]\) is at most \(\frac{2n}{2^B}\). Following lemma 2 that \(\sum_{r=B}^{2^B-1}\frac{n}{2^r} \leq \frac{2n}{2^B}\)

Let \(F\) be the sequence of all the edges traversed in \(m\) findset operations, we need to count the number of edges, which is the total number of cost.

Let \(T_1\) be the set of the edges connected to a root, since each findset will eventually traversed to the root, we have that \(|T_1| = m\).

Let \(T_2\) be the set of the edges that traversed between nodes from different bins. Since the rank on the find path has increasing ranks and we have at most \(\log^*n\) bins, we have \(|T_2| \in O(m\log^*n)\)

Let \(T_3\) be the set of the edges that traversed in the same bin. Consider any edge \((u, v)\), and the nodes \(u, v, v_1, ..., v_k\) on the find path to the root. Then none of the nodes are root, and they will never appear in \(T_3\) since they are directly attached to a root. Also, known that rank is strictly increasing, so that the length of each find path is at most \(2^B-1-B < 2^B\). Therefore, for a bucket \([B, 2^{B-1}]\). The total number of edges is at most \(\frac{2n}{2^B}2^B = 2n\). With at most \(\log^*n\) bins, \(|T_3| = 2n \log^*n\).

Therefore, we can conclude that the worst case amortized run time is \(T(m, n) = |T_1| + |T_2| + |T_3| \in O(m\log^* n)\)

Implementation

DisjointSet implementation 
# Note that this implementation add unnecessary parent for ploting
from .plot_trees import plot_tree, construct_tree_nodes

class DNode:
    def __init__(self, x) -> None:
        self.value = x
        self.rank = 0
        self.parent = self
        # this is only for easy printing
        self.children = []

class DisjointSet:

    def __init__(self) -> None:
        self.nodes = []
        self.n = 0


    def makeset(self, x):
        self.nodes.append(DNode(x))
        self.n += 1

    # path compression
    def findset(self, node):
        if node.parent is node:
            return node
        root = self.findset(node.parent)
        if node.parent is not root:
            root.children.append(node)
            node.parent.children.remove(node)
            node.parent = root
        return root

    def findset_naive(self, node):
        if node.parent is node:
            return node
        return self.findset_naive(node.parent)

    def union(self, x, y):
        sx = self.findset(x)
        sy = self.findset(y)
        if sx is not sy:
            self.__link(sx, sy)
            self.n -= 1

    def union_naive(self, x, y):
        sx = self.findset_naive(x)
        sy = self.findset_naive(y)
        if sx is not sy:
            self.__link_naive(sx, sy)
            self.n -= 1

    def union_weighted(self, x, y):
        sx = self.findset_naive(x)
        sy = self.findset_naive(y)
        if sx is not sy:
            self.__link(sx, sy)
            self.n -= 1

    def union_compression(self, x, y):
        sx = self.findset(x)
        sy = self.findset(y)
        if sx is not sy:
            self.__link_naive(sx, sy)
            self.n -= 1

    # weighted union
    def __link(self, x, y):
        if x.rank > y.rank:
            y.parent = x
            x.children.append(y)
        elif x.rank < y.rank:
            x.parent = y
            y.children.append(x)
        else:
            y.parent = x
            x.children.append(y)
            x.rank += 1

    def __link_naive(self, sx, sy):
        sx.parent = sy
        sy.children.append(sx)
        sy.rank = max(sy.rank, sx.rank + 1)


    def plot(self, label_fn, path):
        counter, i = 0, 0
        root = DNode(r"$\mathcal S$")
        while counter < self.n:
            node = self.nodes[i]
            if node.parent is node:
                root.children.append(node)
                counter += 1
            i += 1
        return plot_tree(construct_tree_nodes(root, label_fn, children_attr="children"), path)

ds = DisjointSet()
for v in range(NV):
    ds.makeset(v)
nodes = ds.nodes
for e in E:
    ds.union(nodes[e[0]], nodes[e[1]])
ds.plot(label_fn, "assets/disjoint_set_6.jpg")

print("Number of connected components", ds.n)
#>> Number of connected components 9

png