Graphs: Depth-first Search

Depth-First Search

Consider a undirected graph $G=(V,E)$ with $|V|=n, |E|=m$

The strategy for DFS is to go as "deeper" as possible. Similar to BFS, we start with all vertices being undiscovered; then we "discover" it when we first encounter it from some vertex's neighborhood; finally, we finish processing a vertex when we finish processing all of its neighbors. Thus, this suggested a recursive algorithm.

We also use a timestamp to record the time when a vertex is discovered as v.d, and when it is finished as v.f. We will explore its uses later in DFS properties.

DFS(G)
for u in G.V:
    u.state = undiscovered
time = 0
for u in G.V:
    if u.state == undiscovered:
        DFS_visit(G, u)

DFS_visit(G, u)
time += 1
u.d = time
u.state = discovered
for v in u.neighbors:
    if v.state == undiscovered:
        DFS_visit(G, v)
u.state = FINISHED
time += 1
u.f = time

Lemma 1 After the execution of DFS, for $v\in V$, $1 \leq v.d < v.f \leq 2n$.
proof. The bound $[1, 2n]$ is trivial. Since timestamp only increment when we discover and finish one vertex. Thus, there are at most $n$ vertices to visit, and we visit each vertex exactly once. Also, note that time cannot decrease, and by DFS_visit line 8, we must have $v.d < v.f$.

Time Complexity

Note that DFS_visit is called on each undiscovered vertex exactly once, and in each DFS_visit, we loop through all of its neighbors once. Thus, the time complexity is $O(n+m)$

Depth First Trees and Depth First Forests

Consider the DFS algorithm, for each recursive call on DFS_visit on line 4-6. we add an edge $(u,v)$. Thus, we have a new graph $G'=(V,E')$. Note that on each search path, we won't go further if the point is already discovered. Therefore, the graph is acyclic, thus it is a forest consisting one or more trees. Calling $G'$ depth first forest_; and the trees within $G' = \{T_1,..., T_k\}$ be the __depth first trees.

Parenthsis Theorem

Theorem 1 For any two vertices $u,v$ we have one of the following conditions - $[u.d, u.f] \cap [v.d, v.f] = \emptyset$, and they are not a descendant of each other in $G'$. - $[u.d, u.f] \subset [v.d, v.f]$, and $u$ is a descendant of $v$ in some depth fisrt tree $T_i$.

proof. WLOG we assume that $u.d < v.d$, then by lemma 1, we have two cases.
$v.d < u.f$, so $v$ was discovered while $u$ haven't finished, which implies that $v$ is a descendant of $u$. Moreover, $v$ must finishes earlier than $u$, otherwise the call stacks won't return.
$u.f < v.d$, then the intervals are disjoint, and $u$ must finish exploration before discovering $v$, thus they are not a descendant of each other.

Corollary 2 If $v$ is $u$'s proper descendant, then $u.d < v.d < v.f <u.f$

White Path Theorem

Theorem 3 In a depth first forest $G'$, $v$ is a descendant of $u$ IFF at the time $u.d$ that the search discovers $u$, there is a path from $u$ to $v$ consisting entirely of undiscoverted vertices.

proof. $\Rightarrow$. If $v=u$, then the path contains only $u$, and it's undiscoverted. Overwise, by corollary 2, $u.d < v.d$ so that $v$ is undiscovered yet.

$\Leftarrow$, consider any path between $u, v$ formed by undiscovered vertices, and $v$ does not become a descendant in $G'$ yet. WLOG assume that every vertex other than $v$ along the path becomes a descendant of $u$. Let $w$ be the predecessor of $v$ in the path so that #w$ is a descendant of $u$. By corollary 2m $w.f \leq u.f$. Because $v$ must be discovered after $u$ is discoverted but before $w$ finishes, we have that $u.d < v.d < w.f \leq u.f$, while $v.f \leq w.f$. Thus, $[v.d, v.f] \subset [u.d, u.f]$, it is a desendant of $u$.

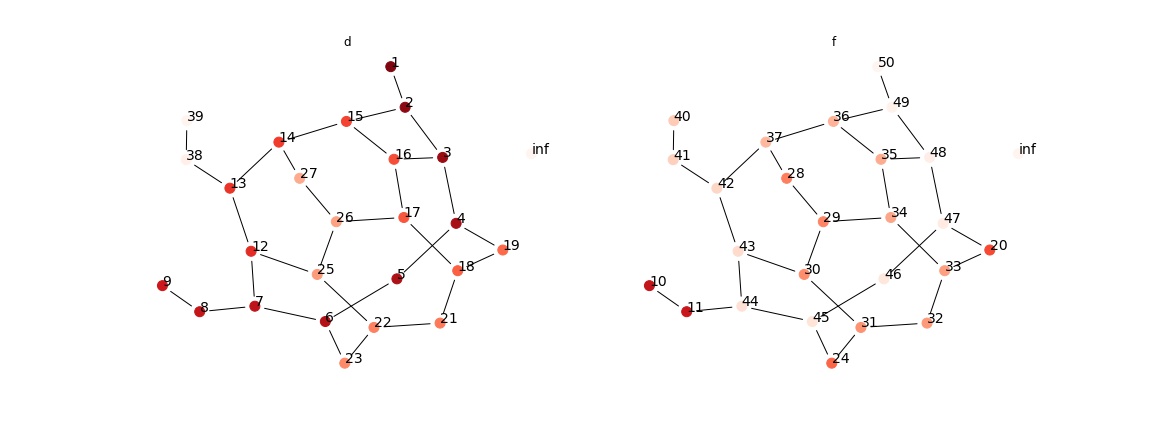
import igraph as ig
# create a example graph, and add one unreachable point
g = ig.Graph.Famous('Walther'); g.add_vertex()
layout = g.layout();

from assets.graph_search import traversal_order, DFS, plot_graph, topological_sort
traversal_order(DFS, g, 0)
plot_graph(g, ['d', 'f'], layout, "assets/dfs_1.jpg")

[+] Topological Sort

Note that both BFS and DFS works the same on directed graph (only need to modify neighbors to all outwards edges).

Now, consider a directed acyclic graph (dag), a topological sort of a dag is a linear ordering of all vertices s.t. if $G$ contains an edge $(u,v)$, then $u$ appears before $v$ in the ordering.

Then, note that DFS iterates through all vertices exactly once, and we have the algorithm for togological sort

topological_sort(G)
# precondition: G is a dag
L = linked_list()
call DFS(G)
for each vertex is finishes, prepend it into L
return L

Obviously, topological_sort runs in $\Theta(V+E)$ as DFS does.

Correctedness

Lemma 4 A directed graph $G$ is acyclic IFF DFS(G) yields no back edges.
proof. $\Leftarrow$ Suppose DFS has a back edge. Then $v$ is an ancestor of $u$ in $G'$. Thus, $G$ contains a path from $v$ to $u$, and we have a cycle $u\rightsquigarrow v \rightarrow u$. $\Rightarrow$ suppose $G$ contians a cycle $C$. Let $v$ be the first vertex to be discovered in $c$, and $(u,v)$ be the preceding edge in $c$. At time $v.d$, the vertices of $c$ from a path of undiscovered vertices from $v$ to $u$. By claim 3, $u$ is a descendant of $v$ in $G'$. Thus, $(u,v)$ is a back edge.

Theorem 5 topological_sort(G) produces a topological sort given a dag $G$.

proof. Note that the order of vertices in $L$ is determined by $v.f$. Thus, we only need to show that for any pair of $u,v\in V, u\neq v$, if $(u,v)\in E$, then $v.f < u.f$.

Consider any edge $(u,v)$ explored by DFS. When this edge is explored, $v$ cannot be discovered but not finished, since then it will produce a back edge, contradicting lemma 4. Therefore, $v$ is either undiscovered or already finished. If $v$ is white, then it becomes a descendant of $u$ and $v.f < u.f$. If $v$ is finished, so that $v.f$ has already been set. But we are still iterating through $u$'s neighbor. Thus, $v.f < u.f$.

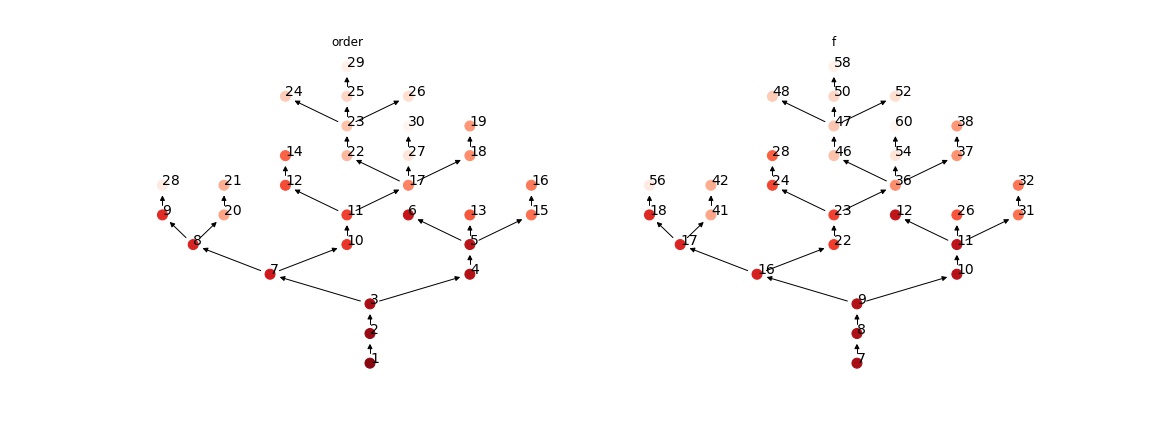
import igraph as ig
# create a example graph, and add one unreachable point
g = ig.Graph.Tree_Game(30, directed=True); 
layout = g.layout("tree");

from assets.graph_search import traversal_order, DFS, plot_graph, topological_sort
topological_sort(g)
plot_graph(g, ['order', 'f'], layout, "assets/dfs_2.jpg")

Circle Detection

A corollary of lemma 4 is that during DFS, if we find a back edge, then it contains a cycle. Note that this proof also applies to undirected graph, if we think of each undirected edge as two directed edge.

Thus, we have the modified DFS_visit for detecting cycle that contains $u$.

DFS_visit_undirected(G, u)
    # ...
    for v in u.neighbors:
        if v.state == undiscovered:
            u.parent = v
            DFS_visit(G, v)
        # u is discovered before so there is a path 
        # between u, v, now this if check gives 
        # that the edge (u, v) is not discovered
        # thus closes the cycle
        elif u != v.parent: 
            raise CYCLE
    # ...

DFS_visit_directed(G, u)
    # ...
    for v in u.neighbors:
        if v.state == undiscovered:
            u.parent = v
            DFS_visit(G, v)
        # if u is discovered but not finished
        # meaning that there is a path from v 
        # to u, now the path is closed by a new
        # (v, u) edge
        elif u.state == discovered: 
            raise CYCLE
    # ...

[+] Stongly Connected Components

Given a graph $G = (V,E)$, the strongly connected component (SCC) of $G$ is a maximal set of vertices $C\subseteq V$ s.t. $\forall u,v \in C. \exists u\rightsquigarrow v, v\rightsquigarrow u$. Note that each vertex itself is a connected component, as it is reachable to itself.

Note that if we have two SCCs $C_1, C_2$, and there exists edges from some vertices in $C_1$ to $C_2$, and $C_2$ to $C_1$, then the SCCs merged into a larger one. Thus, each graph has a unique SCC decomposition.

Define the transpose of some graph $G=(V, E)$ as $G^T = (V, E^T)$ where $E^T = \{(v,u): (u,v) \in E\}$, i.e. reverse all edge directions. Note that this is a transpose because if we represent $G$ using a adjacency matrix, then $G^T$ is the transpose of the adjacency matrix. Note that $G$ and $G^T$ have exactly the same SCC.

Then, the algorithm is as following

DFS(G)
for u in G.V:
    u.state = undiscovered
    time = 0
    for u in G.V:
        if u.state == undiscovered:
            DFS_visit(G, u)

c title="SCC(G)" linenumes="1" DFS(G) to compute u.f for each vertex compute G.T be the transpose DFS(G.T) but line 4 uses decreasing u.f order output vertices of each tree formed by DFS(G.T)

Time Complexity

DFS runs in $O(n+m)$, transpose a graph takes $O(n+m)$ time (reverse all edges in adjacency list). The final output of vertices takes at most $O(n)$ time (When we return from all DFS_visit stacks in DFS, we have already found one completed tree). Thus the total time is still in $O(n+m)$.

Correctedness

Some extra notes: Consider SCC line 3, the decreasing $u.f$ order is actually the topological sorted order.

All the $u.d$ and $u.f$ mentioned here will be referring to SCC line 1. Actually, for SCC line 3 we can omit the timestamps since it is not necessary.

Lemma 6 If $C,C'$ are two distinct SCC in directed graph $G$. Then, if exists some path from $x\in C$ to $x'\in C'$, then we cannot have path from $y\in C$ to $y'\in C'$.
proof. As what our observation.

Then, for $U\subseteq V$, define $d(U) = \min\{u.d: u\in U\}, f(U) = \min\{u.f: u\in U\}$.

Lemma 7 Let $C,C'$ be distinct SCC in $G$. If $\exists (u,v)\in E, u\in C, v\in C'$, then $f(C) > f(C')$.
proof. Consider two cases:
If vertices in $C$ is discovered earlier than $C'$, then $d(C) < d(C')$. Take $x\in C. x.d = d(C)$ be the first dicovered vertex. Then at time $x.d$, all vertices in $C, C'$ are undiscovered. By SCC definition, for any vertex $w\in C'$, exists a white path $x\rightsquigarrow u\rightarrow v\rightsquigarrow w$. By white-path theorem, all vertices in $C$ and $C'$ become descendant of $x$ in $G'$. Thus $x.f = f(C) > w.f \geq f(C')$.

If $d(C') < d(C)$, then by lemma 6 we cannot have a path from vertices $C'$ to vertices in $C$. Thus, all vertices in $C$ is undiscovered until all vertices in $C'$ finishes. Resulting $f(C) > f(C')$.

Corollary 8 Let $C,C'$ be distinct SCC in $G$. If $\exists (u,v)\in E^T, u\in C, v\in C'$, then $f(C) < f(C')$.
proof. exactly the opposite of lemma 7.

Theorem 9 (Correctedness of SCC) SCC correctly produce the SCC of $G$.

proof. We will argue by induction on the number of depth-frst trees found in the DFS of $G^T$, that the first $k$ trees produced by DFS(G.T) is a SCC.

For $k = 0$, then exists no vertices, vacuously true.

For $k > 0$, assume the first $k$ DFT is SCC. Let the root of the $(k+1)$'th tree be $u$, and let $C$ be the SCC that $u$ belongs. By the topological order we have that $u.f = f(C) > f(C')$ for any SCC $C'\neq C$ and has yet to be visited. At time $u.d$, all vertices in $C$ is not discovered, thus by white-path theorem, $\forall v\in C$ are in the depth-first tree rooted at $u$. Moreover, the vertices in first $k$ SCC must been finished. Thus, no vertex in any SCC other than $C$ will be descendant of $u$ during DFS(G.T).

Component Graph

From the observation above, we know that if there are edges incoming and outcoming between two SCCs, then they can be merged into one SCC. Thus, we define a component graph $G^{C} = (V^C, E^C)$ for graph $G$ with SCCs $C_1,...,C_k$. We define $V^C = \{v_1,...,v_k\}$ w.r.t. to each SCC, and exists $(v_i, v_j) \in E^C$ if $(x\in C_i, y\in C_j) \in E$, a.k.a. exists an edge from $C_i$ to $C_j$.

Claim 10 $((G^T)^C)^T = G^C$.
proof. Note that $((G^T)^C)^T = (V^C, ((E^T)^C)^T)$. Consider $(E^T)^C$, $\forall (v_i, v_j) \in E^C. (x\in C_i, y\in C_j) \in E$, thus $(y\in C_j, x\in C_i) \in E^T, (v_j, v_i) \in (E^T)^C, (v_i, v_j) \in ((E^T)^C)^T$

Corollay 11 DFS(G.T) visits $G^C$ in topologically sorted order.
proof. Consider the topological orderness of vertices of $G$, and since $((G^T)^C)^T = G^C$.