[+] Augmented BST (AVL Tree)

Consider our implementation of AVL tree, the height of a node is

Such property depends only on the property of the child nodes and takes constant time to accumulate. Thus, when insert or delete one node, we only need to make a bottom-up updates from the leaf to root. Taking at most \(O(h)\in O(\log n)\) time.

Ordered Set with rank

ADT: Ordered Set

Suppose that we want our set to supports finding the \(k\)th largest (or smallest) element, a.k.a. a ordered set. Thus, we need to support the additional operations.

• rank(A, x): return the rank of \(x\in A\) where \(rank = r\) IFF there are exactly \(r-1\) elements of \(A\) that is smaller than \(x\).
• select(k): return the key of node \(x\) where \(rank(A, x) = k\).

rank and size

Think about BST's property, for each node x, we have that x is larger than all of its left subtree and its right subtree. Then,

1
2
3
4
5
6
7
8

if x is None:
     return 0
if x.parent is None:
    return size(x.left) + 1
if x is left child of x.parent:
    return rank(x.parent) - size(x.right) - 1
else:
    return rank(x.parent) + size(x.left) + 1

If we know the size of each node, we can retrieve rank is \(O(h)\) time.

Thus we can augment the AVL tree with field size, where

Similar to height, it takes constant time and only depends on its child nodes. Thus, when we modify the data structure, we can upadte size in \(O(h)\) time.

select

Then, we apply the same idea for select,

1
2
3
4
5
6
7

left_size = node.left.size
if k == left_size + 1:
    return node
elif k < left_size + 1:
    return select(node.left, k)
else:
    return select(node.right, k - left_size)

for some node \(x\), it is larger than its left subtree, thus at least larger than \(size(x.\text{left})\). Then, if the wanted node is in the right subtree, we know it is at least the size of the left subtree plus the node.

from assets.AVL import *
from assets.plot_trees import plot_tree, construct_tree_nodes

def compute_size(node):
    if node is None:
        return 0
    node.size = compute_size(node.l) + compute_size(node.r) + 1
    return node.size

def rank(node):
    if node is None:
        return 0
    get_size = lambda node: 0 if node is None else node.size
    if node.parent is None:
        return get_size(node.l)
    if node.parent.l is node:
        return rank(node.parent) - get_size(node.r) - 1
    else:
        return rank(node.parent) + get_size(node.l) + 1

def select(node, k):
    left_size = node.l.size + 1 if node.l is not None else 1
    if left_size == k:
        return node.k
    elif left_size > k:
        return select(node.l, k)
    else:
        return select(node.r, k - left_size) 

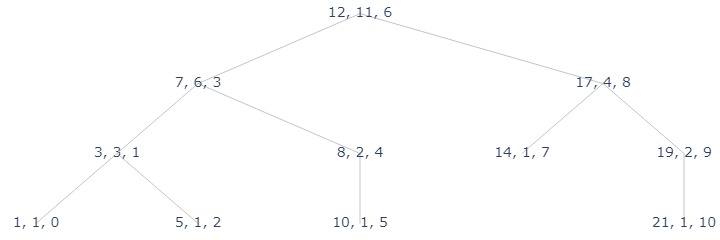
# a demonstration of BST
arr = [12, 3, 17, 1, 7, 14, 19, 5, 8, 10, 21]
root = AVL_insert(None, arr[0])
for x in arr[1:]:
    new_node = AVL_insert(root, x)

compute_size(root)

label_fn = lambda node: f"{node.k}, {node.size}, {rank(node)}"

plot_tree(
    construct_tree_nodes(root, label_fn, ['l', 'r']),
    "assets/avl_app_1.jpg"
)
# key, size, rank

print([select(root, i) for i in range(1, len(arr) + 1)])
#>> [1, 3, 5, 7, 8, 10, 12, 14, 17, 19, 21]