Skip to content

Set: AVL Tree

Abstract Data Type: Set

  • Object:
    • Set \(S\) of keys (distinct integers)
  • Operations:
    • delete(x) removes \(x\) from the set.
    • insert(x) add x to \(S\).
    • search(x) return if \(x\) is in the set.

Note that a dictionary is just a set, instead of storing keys, dictionary stores key value pairs.

Binary Search Tree

Binary search tree is the most basic way to implement a set. However, in worst case, delete, insert, search all take \(O(n)\) time. For example, inserting a sequence of increase numbers, the BST will become a chain.

BST basic implementation
BST.py
class BSTNode:

    # Constructor to create a new node
    def __init__(self, key):
        self.k = key
        self.l = None
        self.r = None

def insert(node, k):

    # If the tree is empty, return a new node
    if node is None:
        return BSTNode(k)

    # Otherwise recur down the tree
    if k < node.k:
        node.l = insert(node.l, k)
    else:
        node.r = insert(node.r, k)

    # return the (unchanged) node pointer
    return node


def search(node, k):
    if node is None:
        return False
    if node.k == k:
        return True
    if k < node.k:
        return search(node.l, k)
    else:
        return search(node.r, k)

def delete(node, k):
    if node is None:
        return node
    if k < node.k:
        node.l = delete(node.l, k)
    elif k > node.k:
        node.r = delete(node.r, k)
    elif node.l is None:
        temp = node.r
        node = None
        return temp
    elif node.r is None:
        temp = node.l
        node = None
        return temp
    else:
        temp = node.r
        while temp.l is not None:
            temp = temp.l
        node.k = temp.k
        node.r = delete(node.r, temp.k)
    return node

from assets.AVL import *
from assets.plot_trees import plot_tree, construct_tree_nodes
from IPython.display import Image
label_fn = lambda x: x.k

# in worst case, it becomes a chain
arr = [1, 2, 3, 4, 5, 6]
root = BST_insert(None, arr[0])
for x in arr[1:]:
    BST_insert(root, x)
plot_tree(
    construct_tree_nodes(root, label_fn, ['l', 'r']),
    "./assets/avl_1.jpg"
)

png

AVL Tree

For AVL tree \(T\), for node \(u\in T\). Define \(h(u)\) be the height of \(u\), a.k.a. the shortest path from \(u\) to a leaf.
Define tree height \(H(T) = h(\text{root}), H(\emptyset) = -1\)

Define balance factor \(BF(u) = H(T_{u,l}) - H(T_{u,r})\) where \(T_{u,l}, T_{u,r}\) are the left subtree and right subtree of \(u\).

Finally, a AVL Tree \(T\) is a BST s.t. \(\forall u\in T. BF(u) \in \{-1, 0, 1\}\).

Properties

Claim 1 Let \(f(h)\) be the smallest number of nodes in a AVL tree of height \(h\). Then, \(f(h) = f(h-1) + f(h-2) + 1\).
proof. Left subtree + Right subtree + root, by balance factor constraint, the subtree height difference can be at most 1.

Claim 2 Let \(F\) be Fibonacci series function, \(F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2}\). Then \(f(h) = F(h+3) - 1\).

proof.

\[\begin{align*} f(0) &= F_3 - 1 = F_2 + F_1 - 1 = 1\\ f(1) &= F_4 - 1 = 3 - 1 = 2\\ f(h) &= f(h-1) + f(h-2) + 1 \\ &= F_{h+2} -1 + F_{h+1} -1 + 1 = F_{h+3} - 1 \end{align*}\]

Claim 3 \(h \in O(\log n)\).
proof. Let \(n\) be the number of nodes, \(h\) be the height

\[\begin{align*} n &\geq f(h) \\ &= F_{h+3} - 1 \\ &= \frac{(1+\sqrt{5})^{h+3} - (1-\sqrt{5})^{h+3}}{2^{h+3}\sqrt 5 } - 1\\ &\geq \frac{1}{\sqrt 5}(\frac{1+\sqrt{5}}{2})^{h+3} - 2\\ \sqrt{5}(n+2)&\geq (\frac{1+\sqrt{5}}{2})^{h+3}\\ \log_{\frac{1+\sqrt{5}}{2}}\sqrt{5}(n+2) &\geq h+3\\ h &\leq \log_{\frac{1+\sqrt{5}}{2}}\sqrt{5}(n+2) -3\\ h&\in O(\log n) \end{align*}\]

insert

Consider the major properties of AVL tree. We want it to be a self-balanced BST. Therefore, after inserting an element as of regular BST, we want to make the tree balance.

AVL_insert(root, x)
    #precondition: root is the root of a AVL tree
    #postcondition: root is the root of a AVL tree containing x
 1  new_leaf = BST_insert(root, x)
 2  curr = new_leaf
 3  while curr is not root:
 4      BF = height(curr.right) - height(curr.left)
 5      if BF == 0:
 6          return
 7      elif BF == 2 or BF == -2:
 8          fix_imbalance(curr)
 9          return
10      update curr height
11      curr = curr.parent

Correctness

First note that by our definition of height, only \(x\)'s ancestors will need to update their height, and hence balance factor.

Intuitively, there are 3 cases in the while loop

BF = 0: the newly added node makes the tree balanced. Thus, the lighter of the two subtrees add one node \(x\). This means that the current node's height won't change, since its height is max(height(curr.left), height(curr.right)) + 1. Thus, current node's ancestors won't need to update their height.

BF = 1 or BF = -1: AVL tree property is not violated, but the height need to be updated, hence we have to continue on looking up.

BF = 2 or BF = -2: AVL tree property got violated, we need to fix the imbalance on the branch, while maintaining BST properties. Moreover, we can make the current node's balance factor 0 after fix_imbalance, thus we can stop the while loop.

Runtime

BST_insert takes \(O(h)\) time. Each iteration of the while loop, the depth of the curr reduces by 1. Thusm there are at most \(h\) iterations. In each iteration, all branches take constant time. Thus, each insert is \(\in O(h)\). Then, by AVL tree's self-balancing property claim 3, we have \(\in O(\log n)\)

Rotation

left_rotate and right_rotate can modify the BST in \(O(1)\) time, maintaining the BST property.

right_rotate(root)
 1  r = root.right
 2  rl = r.left
 3  root.right = rl
 4  r.left = root
 5  root = r
left_rotate(root)
 1  l = root.left
 2  lr = l.right
 3  root.left = lr
 4  l.right = root
 5  root = l

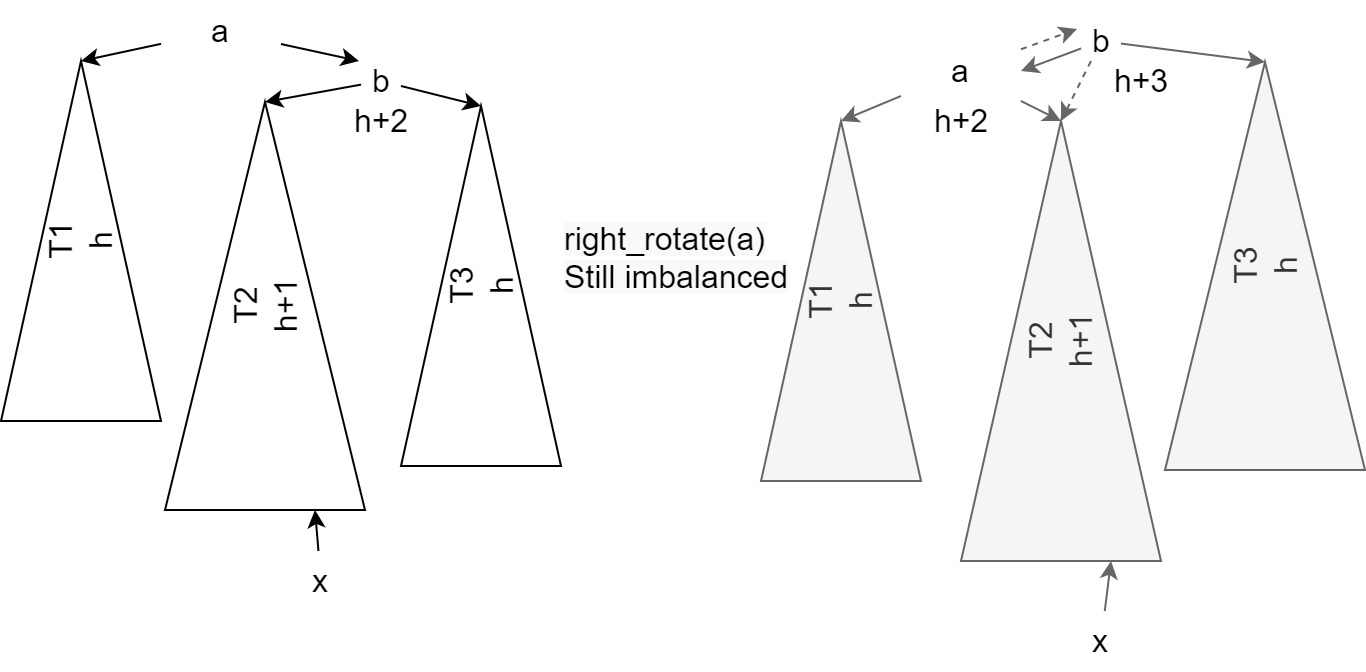
Given an imbalanced BST with \(\pm 2\) BF on root, and \(\pm 1, 0\) BF on other nodes. We want a new BST that is balanced. WLOG assume the right subtree is heavier. There are two cases

right, right case: right subtree of right subtree is heavier. This is easy since after one right_rotate, it is balanced.

right, left case: if we do a right rotation, then it is still imbalanced. Thus, the idea is first left rotate the right subtree, so that the right subtree's right is heavier. Then, we go back to right, right case.

right_rotate balanced

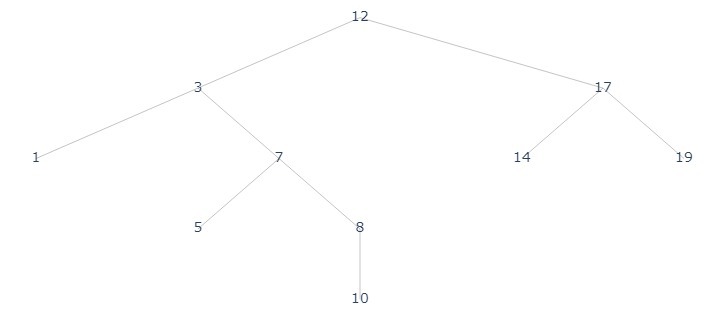
# a demonstration of BST
arr = [12, 3, 17, 1, 7, 14, 19, 5, 8, 10]
root = BST_insert(None, arr[0])
for x in arr[1:]:
    new_node = BST_insert(root, x)
    BST_update_height(new_node)
plot_tree(
    construct_tree_nodes(root, label_fn, ['l', 'r']),
    "assets/avl_2.jpg"
)

png

right_rotate(root.l)
plot_tree(
    construct_tree_nodes(root, label_fn, ['l', 'r']),
    "assets/avl_3.jpg"
)

png

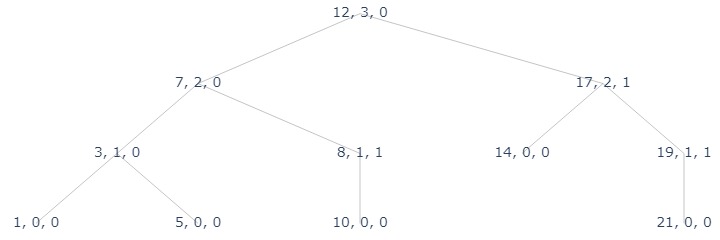
# a demonstration of BST
arr = [12, 3, 17, 1, 7, 14, 19, 5, 8, 10, 21]
root = AVL_insert(None, arr[0])
for x in arr[1:]:
    new_node = AVL_insert(root, x)
label_fn = lambda node: f"{node.k}, {get_height(node)}, {get_BF(node)}"
plot_tree(
    construct_tree_nodes(root, label_fn, ['l', 'r']),
    "assets/avl_4.jpg"
)
# key, height, BF

png

[+] delete

The idea is similar to insert, but need more considerations on the details.

First, BST_insert will only delete leaf node (otherwise swap child node until the to be deleted node is a leaf). Thus, call the to be deleted lead node x, then we trace up from x.parent to root as curr and consider the cases

  1. if curr's old BF is \(0\), then removal x will shorten one of is subtree, but curr.height won't change. Thus, if BF changes from \(0\rightarrow \pm 1\), we are safe to stop.
  2. if curr's old BF is \(\pm 1\), then the new BF will either be \(0\) or \(\pm 2\).
  3. In the case of \(0\), curr.height will update and we still need to go up.
  4. In the case of \(\pm 2\), we will rotate to fix imbalance. fix_imbalance will update height thus we need to go up.

The correctness and runtime justification is very similar to insert.

Fix Imbalance

Imbalance happens when we delete a node from the lighter subtree, and there are 3 cases to consider. As shown below

delete case 1, 2